P(x)=5x⁵y²
Q(x)=15x³y⁴
Olduğuna göre OBEB[P(x),Q(x)] Cevap: 5x³y²
P(x) bir pol.olmk.üzere:
ise P(x) in x²-4 ile bölünmesiyle kalan polinomun katsayılar toplamı kaçtır? Cevap:0
n pozitif bir tam sayı ve Q(x)≠0 olm.üzr.
P(x)=(1+x)n.(1-x)²
der[P(x).Q(x)]=8-n
olduğuna göre der[Q(x)] en çok kaçtır? Cevap:4
Q(x)=15x³y⁴
Olduğuna göre OBEB[P(x),Q(x)] Cevap: 5x³y²
P(x) bir pol.olmk.üzere:
P(2)
P(-2)
=
1
3
ise P(x) in x²-4 ile bölünmesiyle kalan polinomun katsayılar toplamı kaçtır? Cevap:0
n pozitif bir tam sayı ve Q(x)≠0 olm.üzr.
P(x)=(1+x)n.(1-x)²
der[P(x).Q(x)]=8-n
olduğuna göre der[Q(x)] en çok kaçtır? Cevap:4
svsmumcu26 15:09 24 Şub 2013 #2
1.
İkisindede ortak olan terimleri arıyoruz.
Q(x)=3.5.x^3.y^2.y^2 olarak yazılabilir görüldüğü üzere 5x^3y^2 ikisindede ortak terim olur.
2.
3.P(2)=P(-2)
P(x)=(x-2).(x+2).Q(x)+mx+n
Bu kısımdan sonra P(2) ve P(-2) için çözülürse cevaba ulaşılır bunuda size bırakalım.
3.
x^n+2 , p(x)'in derecesidir Q(x)'in derecesi -2n+6 olur. n+2 Q(x)'in derecesiydi n=1 için x^3 olur -2n+6 => n=1 di => 4 olur Q(x)'in derecesi bu da maximumdur.
İkisindede ortak olan terimleri arıyoruz.
Q(x)=3.5.x^3.y^2.y^2 olarak yazılabilir görüldüğü üzere 5x^3y^2 ikisindede ortak terim olur.
2.
3.P(2)=P(-2)
P(x)=(x-2).(x+2).Q(x)+mx+n
Bu kısımdan sonra P(2) ve P(-2) için çözülürse cevaba ulaşılır bunuda size bırakalım.
3.
x^n+2 , p(x)'in derecesidir Q(x)'in derecesi -2n+6 olur. n+2 Q(x)'in derecesiydi n=1 için x^3 olur -2n+6 => n=1 di => 4 olur Q(x)'in derecesi bu da maximumdur.
Bir de bu soruyu çözer misiniz?
svsmumcu26 15:58 24 Şub 2013 #4
4.
Neyi soruyor ? Denklemini mi ? Tam olarak yazınız sorularınızı.
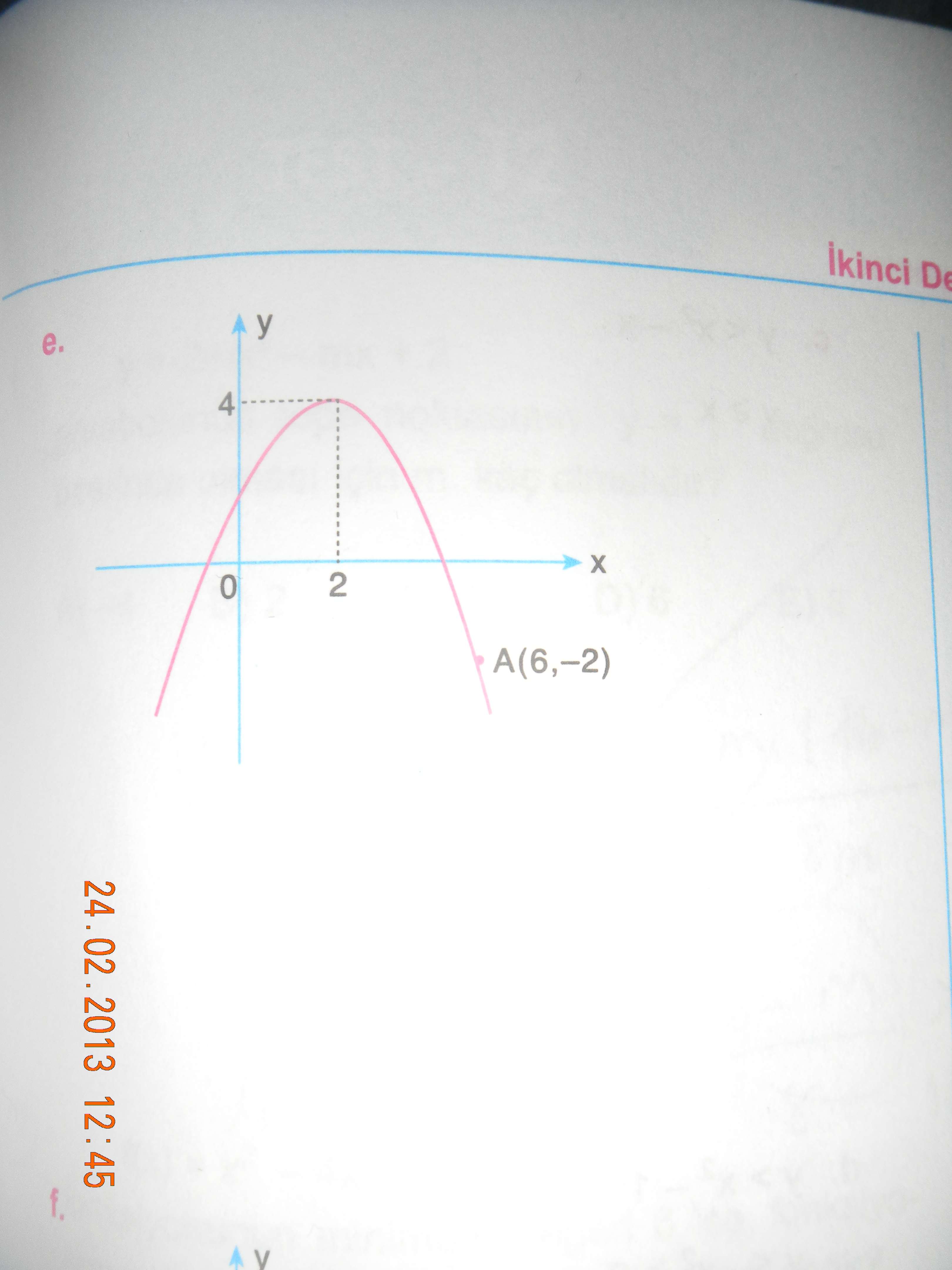
Eğer denklemini soruyorsa bu parabol orjinden +2 birim x ekseninde oynatılmış sonrada 4 br yukarı çıkarılmış bi paraboldür.
O halde genel denklemi y=a.(x-2)^2+4 şeklindedir.
Görüldüğü üzere A(6,-2) noktasından da geçiyormuş o halde nokta parabol denklemini sağlamalıdır. (-2)=a.(4)^2+4 => -6=16.a => a=-6/16 = -3/8 olduğuda bulunmuş olur.
MustafaYağcının sitesine girip MYMat 2'den parabol denkleminin yazılması makalesini okuyun.
Neyi soruyor ? Denklemini mi ? Tam olarak yazınız sorularınızı.
Eğer denklemini soruyorsa bu parabol orjinden +2 birim x ekseninde oynatılmış sonrada 4 br yukarı çıkarılmış bi paraboldür.
O halde genel denklemi y=a.(x-2)^2+4 şeklindedir.
Görüldüğü üzere A(6,-2) noktasından da geçiyormuş o halde nokta parabol denklemini sağlamalıdır. (-2)=a.(4)^2+4 => -6=16.a => a=-6/16 = -3/8 olduğuda bulunmuş olur.
MustafaYağcının sitesine girip MYMat 2'den parabol denkleminin yazılması makalesini okuyun.
Çok Çok sağol
svsmumcu26 16:06 24 Şub 2013 #6
Rica Ederim.
Gir o siteye makaleleri oku garanti anlarsın.
Gir o siteye makaleleri oku garanti anlarsın.