S-1)
k bir gercel sayı olmak uzere her x gercel sayisi icin
f(x)=kx²-4kx+4k+4
Parabollerninin gectigi sabit noktanin apsisi kactir? (2)
S-2)
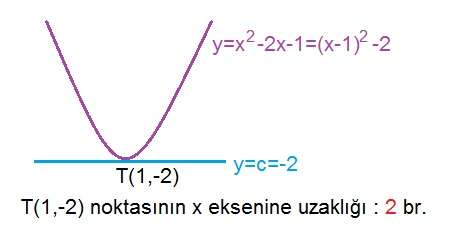
y=x²-2x-1
Parabolune cizilen y=c tegetinin x eksenine uzakligi kactir? (2)
S-3)
y=x²-(2m+2)-m²
Parabollerinin tepe noktalarinin geometrik yer denklemini bulunuz.
S-4)
x=2y² ve y =2x²
Egrilerinin kesim noktalarinin ordinatlar toplami kactir?(1/2)
k bir gercel sayı olmak uzere her x gercel sayisi icin
f(x)=kx²-4kx+4k+4
Parabollerninin gectigi sabit noktanin apsisi kactir? (2)
S-2)
y=x²-2x-1
Parabolune cizilen y=c tegetinin x eksenine uzakligi kactir? (2)
S-3)
y=x²-(2m+2)-m²
Parabollerinin tepe noktalarinin geometrik yer denklemini bulunuz.
S-4)
x=2y² ve y =2x²
Egrilerinin kesim noktalarinin ordinatlar toplami kactir?(1/2)
5
ikisinden de y yi çekelim.
y=√(x/2)
y=2x²
4x⁴=x/2
8x⁴=x
8x⁴-x=0
x(8x³-1)=0
x=0
x=(1/2)
y=√x/2
y=√1/4
y=1/2
ikisinden de y yi çekelim.
y=√(x/2)
y=2x²
4x⁴=x/2
8x⁴=x
8x⁴-x=0
x(8x³-1)=0
x=0
x=(1/2)
y=√x/2
y=√1/4
y=1/2
S-3)
y=x²-(2m+2)x-m²
Parabollerinin tepe noktalarinin geometrik yer denklemini bulunuz.[sanırım 2m+2 nin yanında xi unutmuşsun]
r=(2m+2)/2=m+1
k yı bulmak için x=m+1 i denkleme yazarız ve k=(m+1)²-2(m+1)²-m²
k=-(m+1)²-m²
k=-r²-(r-1)²
ozaman denklem
y=-x²-(x-1)² olur.
y=x²-(2m+2)x-m²
Parabollerinin tepe noktalarinin geometrik yer denklemini bulunuz.[sanırım 2m+2 nin yanında xi unutmuşsun]
r=(2m+2)/2=m+1
k yı bulmak için x=m+1 i denkleme yazarız ve k=(m+1)²-2(m+1)²-m²
k=-(m+1)²-m²
k=-r²-(r-1)²
ozaman denklem
y=-x²-(x-1)² olur.
Tesekkurler arkadaslar..
Diger sorular icin Guncel..
Diger sorular icin Guncel..
C-1
Parabolde parametre k olduğundan, farklı k değerleri için iki tane parabol yazalım.
k=1 ve k=2 için paraboller oluşturalım,
k=1 için,
x²-4x+8
k=2 için,
2x²-8x+12
İki parabolü birbirine eşitleyip ortak çözüm denklemi oluşturalım.
x²-4x+8=2x²-8x+12
x²-4x+4=0
(x-2)²=0
x=2 bulunur.
y değerini de şu şekilde buluyoruz,
y=x²-4x+8
y=2x²-8x+12
+_________
2y=3x²-12x+20
x=2 için,
2y=12-24+20
2y=8
y=4
Parabollerin geçtiği sabit nokta (2,4) noktasıdır.
Parabolde parametre k olduğundan, farklı k değerleri için iki tane parabol yazalım.
k=1 ve k=2 için paraboller oluşturalım,
k=1 için,
x²-4x+8
k=2 için,
2x²-8x+12
İki parabolü birbirine eşitleyip ortak çözüm denklemi oluşturalım.
x²-4x+8=2x²-8x+12
x²-4x+4=0
(x-2)²=0
x=2 bulunur.
y değerini de şu şekilde buluyoruz,
y=x²-4x+8
y=2x²-8x+12
+_________
2y=3x²-12x+20
x=2 için,
2y=12-24+20
2y=8
y=4
Parabollerin geçtiği sabit nokta (2,4) noktasıdır.
1)
Gökberk, daha kısa olsun:

Gökberk, daha kısa olsun:

2)

Tesekkrler gokberk.
Hocam cok saolun , bu sekilde paranteze aldim da parabol denklemi olduguna hic dikkat etmemisim tekrar tesekkur ederim. 2. Soru kaldi bir de ona bakar misiniz ?
tekrar tesekkur ederim. 2. Soru kaldi bir de ona bakar misiniz ?
Hocam cok saolun , bu sekilde paranteze aldim da parabol denklemi olduguna hic dikkat etmemisim
Ben yazana kadar çözmüşsünuz bile  elinize saglik cok saolun.
elinize saglik cok saolun.
