Arkadaşlar yardımınızı bekliyorum
1) lx²-3x-4l≤lx+1l eşitsizliğini sağlayan x in tamsayı değerleri kaç tanedir? cvp:4
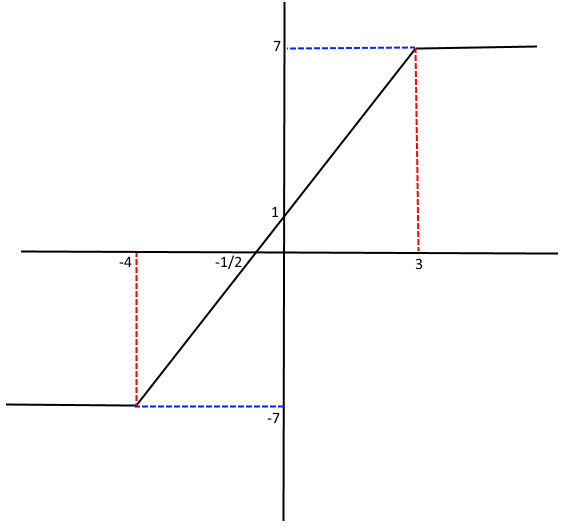
2) A=lx+4l-lx-3l olduğuna göre A nın alabileceği kaç farklı tamsayı değeri vardır? cvp:15
3) 5.lx-2l+7.l4-2xl=10! denklemini sağlayan x değerleri toplamı nedir? cvp:4
Teşekkürler