mutlak değer soruları

Arkadaşlar yardımınızı bekliyorum

1) lx²-3x-4l≤lx+1l eşitsizliğini sağlayan x in tamsayı değerleri kaç tanedir? cvp:4

2) A=lx+4l-lx-3l olduğuna göre A nın alabileceği kaç farklı tamsayı değeri vardır? cvp:15

3) 5.lx-2l+7.l4-2xl=10! denklemini sağlayan x değerleri toplamı nedir? cvp:4

Teşekkürler

1
İki mutlak değer eşitse ya aynı şekilde eşittirler ya da biri diğerinin eksilisine eşittir..|a|=|b| ise a=b veya a=-b
Her iki durumu da inceleyelim..
lx²-3x-4l≤lx+1l
x²-3x-4≤x+1
x²-4x-5≤0
(x-5)(x+1)≤0
eşitsizlik tablosu çizelim..

++++[-1]------[5]+++++
[-1,5] aralığını bulduk..Bulduğumuz değerlerden mutlak değeri sağlayanları çözüm kümemize dahil edeceğiz..
{-1,3,4,5} sağlayan değerler..
x²-3x-4≤-x-1
x²-2x-3≤0
(x-3)(x+1)≤0
eşitsizlik tablosu zaten üstteki tablonun içinde olduğundan tekrar incelemeye gerek yok..
Ç.K.={-1,3,4,5}

2
A=lx+4l-lx-3l ifadesinin alabileceği değerler kısa yoldan şöyle bulunur..
Her iki mutlak değeri 0 yapan x değeri yerine yazılır..Sonuçlar bulunur,bu sonuçlar dahil olmak üzere aradaki bütün sayılar A'nın alabileceği değerlerdir..
x=-4 için
A=|-4+4|-|-4-3|=-7
x=3 için
A=|3+4|-|3-3|=7
[-7,7] aralığındaki tüm değerleri alır..Negatif 7 değer,arada 1 tane 0 var,pozitif 7 değer toplam 7+1+7=15 farklı değer alabilir..
Tabii bu yol tamamen ezber,mantığı biraz uzun sürecek sanırım..
Uzun yolu sadece mantığı kavramak açısından yazıyorum,sınavlarda üstteki yöntem yeterlidir..

Şimdi A=lx+4l-lx-3l bu ifade bir fonksiyon belirtir..Çünkü bir kuralı var,A yerine f(x) yazarsak
f(x)=|x+4|-|x-3| olur..Demek ki fonksiyonmuş..Bu fonksiyonu çözelim..
Kaç farklı çözümü var ? x<-4 için,-4≤x<3 için,3≤x için olmak üzere 3 farklı çözümü var..
x<-4 için her iki ifadenin içi de negatif olur..Bu yüzden iki mutlak değer de işaret değiştirerek çıkar..
-x-4-(-x+3)=-7 bulunur..Demek ki x,-4'ten küçük değerler aldığında sonuç daima -7 bulunuyor..

-4≤x<3 için ilk mutlak değer pozitif,ikincisi negatif olur..Bu yüzden ilki aynen çıkar,ikincisi işaret değiştirerek..
x+4-(-x+3)=2x+1 bulunur..Bu bize şunu anlatıyor..x yukarıdaki aralıktaki değerleri aldığında sonuçlar 2x+1 doğrusunda aynı x değerlerini yazdığımızda oluşacak sonuçlara eşittir..
Örneğin x=0 için doğruda da mutlak değerde de sonuç 1 çıkar..

3≤x için her iki mutlak değerin içi de pozitif olacağından aynen çıkarlar..
x+4-(x-3)=7 bulunur..Buna göre x, 3 ve 3'ten büyük değerler aldığında sonuç daima 7 çıkıyormuş..

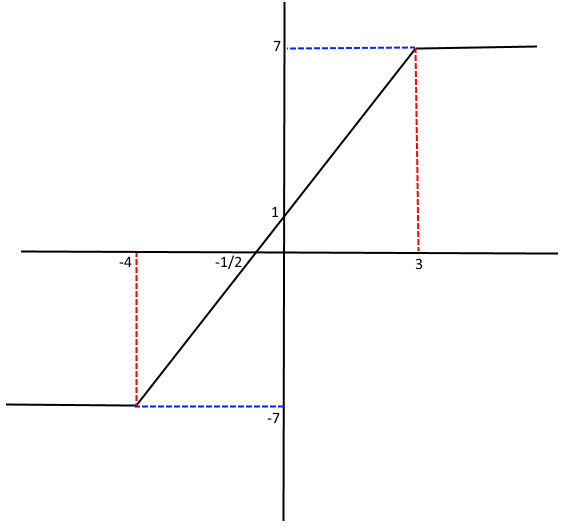
Toparlarsak..x -4 ve 3 aralığındaki tüm değerler için 2x+1 doğrusuna göre sonuç alır,sonuçlar da -7 ve 7 aralığındaki tüm değerleri alır..Buna göre toplam 15 farklı sonuç (y) değerimiz olacaktır..

Altta grafik var daha iyi anlaşılması için..Ancak dikkat edilecek bir nokta var..
x<-4 için sonuç -7 olurken x=-4 için de -7 oldu..x<-4 ifadesinde -4 dahil değil neden -7 oldu diye kafa karışmasın..Biz o -7 sonucunu; -4≤x<3 ifadesi sonucu oluşan 2x+1'de x=-4 için bulduk..Çünkü x'in -4 değerini alabildiği aralık bu aralık,bu aralığın sonucu olan doğruya göre çözmeliyiz..





3
5|x-2|+7|2(2-x)|=10! (7|2(2-x)| ifadesinde mutlak değer özelliğinden 7.|2|.|2-x| yazabiliriz,|2| ifadesi 2 olarak çıkar)
5|x-2|+14|2-x|=10! (|2-x|=|x-2|)
19|x-2|=10! olmadı

Mutlak Değer Soruları ve Çözümleri
Tüm Etiketler