1)|3x-7|< 3 eşitsizliğini sağlayan x tam sayıları toplamı kaçtır? cevap 5
2)|x-3|.|x+3|< 14 eşitsizliğini sağlayan x tam sayı değerlerinin toplamı kaçtır? cevap 0
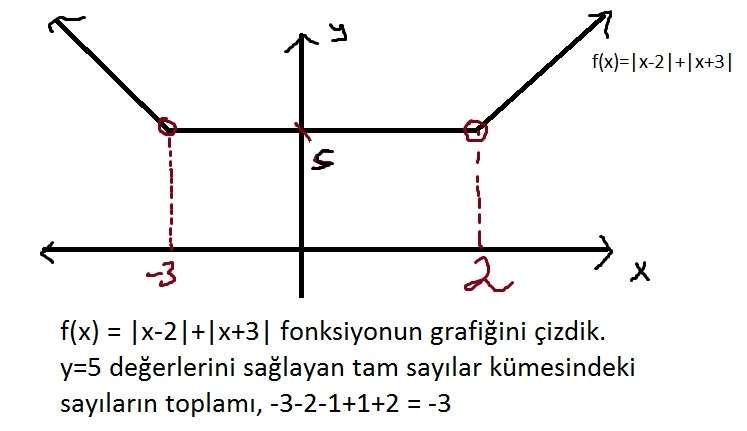
3) |x-2|+ |x+3|= 5 denklemini sağlayan x değerleri toplamı kaçtır? cevap -3
4) |2x+a|≤ 5 eşitsizliğinin çözüm kümesi [-13,-8] olduğuna göre a kaçtır? cevap 21