sanşaynşikro 00:30 30 Kas 2013 #1
1)|3x-7|< 3 eşitsizliğini sağlayan x tam sayıları toplamı kaçtır? cevap 5
2)|x-3|.|x+3|< 14 eşitsizliğini sağlayan x tam sayı değerlerinin toplamı kaçtır? cevap 0
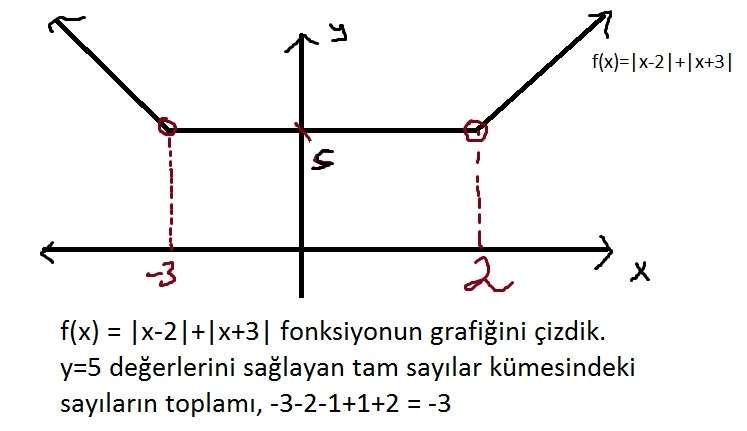
3) |x-2|+ |x+3|= 5 denklemini sağlayan x değerleri toplamı kaçtır? cevap -3
4) |2x+a|≤ 5 eşitsizliğinin çözüm kümesi [-13,-8] olduğuna göre a kaçtır? cevap 21
2)|x-3|.|x+3|< 14 eşitsizliğini sağlayan x tam sayı değerlerinin toplamı kaçtır? cevap 0
3) |x-2|+ |x+3|= 5 denklemini sağlayan x değerleri toplamı kaçtır? cevap -3
4) |2x+a|≤ 5 eşitsizliğinin çözüm kümesi [-13,-8] olduğuna göre a kaçtır? cevap 21
eXCeLLeNCe 19:58 30 Kas 2013 #2 1) |3x-7|<3
|f(x)|<n ise, -n < f(x) < n
-3<3x-7<3
Eşitsizliğin her iki tarafına 7 eklersek; 4<3x<10 olur.
Her tarafı 3 ile bölelim,
4/3<x<10/3
Şimdi 4/3 ile 10/3 arasındaki tamsayıları inceleyelim. Bunu daha iyi inceleyebilmek için sayıları basit kesirlere ayırmanı tavsiye ederim.
1+1/3<x<3+1/3 --> x in eşitsizliği sağladığı değerler: 2,3 toplamları da 5 tir.
|f(x)|<n ise, -n < f(x) < n
-3<3x-7<3
Eşitsizliğin her iki tarafına 7 eklersek; 4<3x<10 olur.
Her tarafı 3 ile bölelim,
4/3<x<10/3
Şimdi 4/3 ile 10/3 arasındaki tamsayıları inceleyelim. Bunu daha iyi inceleyebilmek için sayıları basit kesirlere ayırmanı tavsiye ederim.
1+1/3<x<3+1/3 --> x in eşitsizliği sağladığı değerler: 2,3 toplamları da 5 tir.
eXCeLLeNCe 20:15 30 Kas 2013 #3 3)
eXCeLLeNCe 20:24 30 Kas 2013 #4 4)
|2x+a|≤5
-5≤2x+a≤5
-5-a≤2x≤5-a
(-5-a)/2≤x≤(5-a)/2
ifadesinin çözüm kümesini [-13,-8] vermiş soruda. O halde sınırlardan birini incelersek;
-5-a=-26
5+a=26
a=21
|2x+a|≤5
-5≤2x+a≤5
-5-a≤2x≤5-a
(-5-a)/2≤x≤(5-a)/2
ifadesinin çözüm kümesini [-13,-8] vermiş soruda. O halde sınırlardan birini incelersek;
-5-a=-26
5+a=26
a=21
eXCeLLeNCe 20:34 30 Kas 2013 #5
2) bu soruda tablo oluşturup kökleri yerine yaz, sonra aynı aralıktaki değerleri çarparsan 3 tane 2. dereceden denklem elde edersin, bunların diskriminantını inceleyerek sağladığı aralığı bulabilirsin.