1.soru
x³-2|x|-2=0 denkleminin bir kökü aşağıdaki aralıkların hangisindedir?
A- (-2,-1)
B- (-1,0)
C- (0,1)
D- (1,2)
E- (2,3)
2.soru
(-3∏'den 3∏'ye kadar) ∫sin3xdx/(x²+1) integralinin değeri kaçtır?
cevap 0
3. soru
i²=-1 ve 0<x<2∏ olmak üzere,
(cosx+isinx)³=(cosx-isinx)²
x'in alabileceği değerler toplamı kaçtır? (cevap 4∏ )
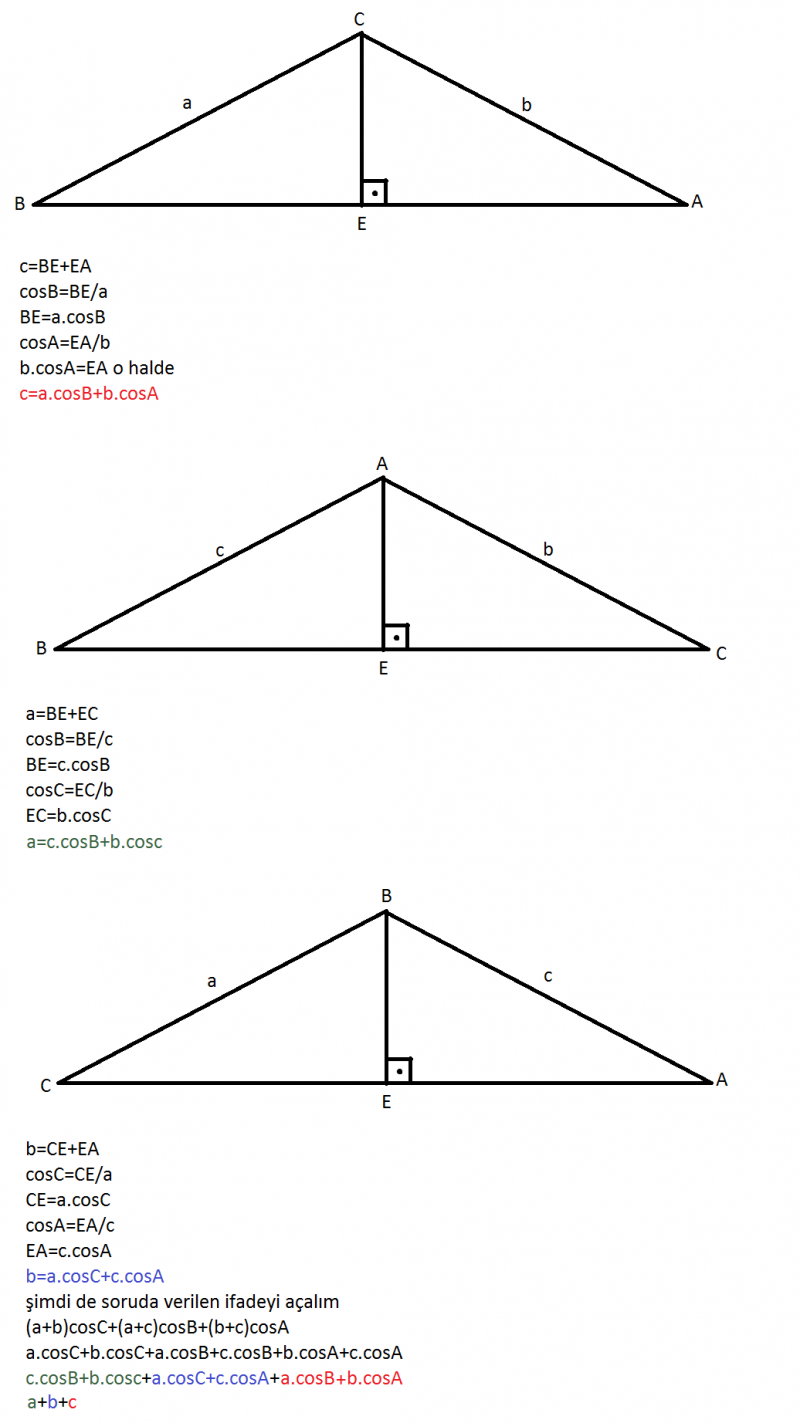
4.soru
Bir ABC üçgeninde A,B,C açılarının karşılarındaki kenar uzunlukları sırasıyla a br,b br ve c br dir.
buna göre, (a+b)cosC+(a+c)cosB+(b+c)cosA toplamı hangisine eşittir?
cevap (a+b+c)
5.soru
sin2x=-2x/11 denkleminin reel sayılarda kaç farklı kökü vardır?
cevap 7
6.soru
(3∏/4'den ∏'ye kadar)∫4dx/(1-tanx) integralinin değeri kaçtır?
7. soru
f(x)=2^x ve g(x)=x+3 fonksiyonları veriliyor.
lim (x---->2)[(f ⁻¹og)(x)]=m olduğuna göre m gerçel sayısı aşağıdaki aralıkların hangisindedir?
A- (0,1)
B- (1,2)
C- (2,3)
D- (3,4)
E- (4,5)