karma sorular

1.soru

x³-2|x|-2=0 denkleminin bir kökü aşağıdaki aralıkların hangisindedir?
A- (-2,-1)
B- (-1,0)
C- (0,1)
D- (1,2)
E- (2,3)

2.soru

(-3∏'den 3∏'ye kadar) ∫sin3xdx/(x²+1) integralinin değeri kaçtır?

cevap 0

3. soru

i²=-1 ve 0<x<2∏ olmak üzere,

(cosx+isinx)³=(cosx-isinx)²
x'in alabileceği değerler toplamı kaçtır? (cevap 4∏ )

4.soru

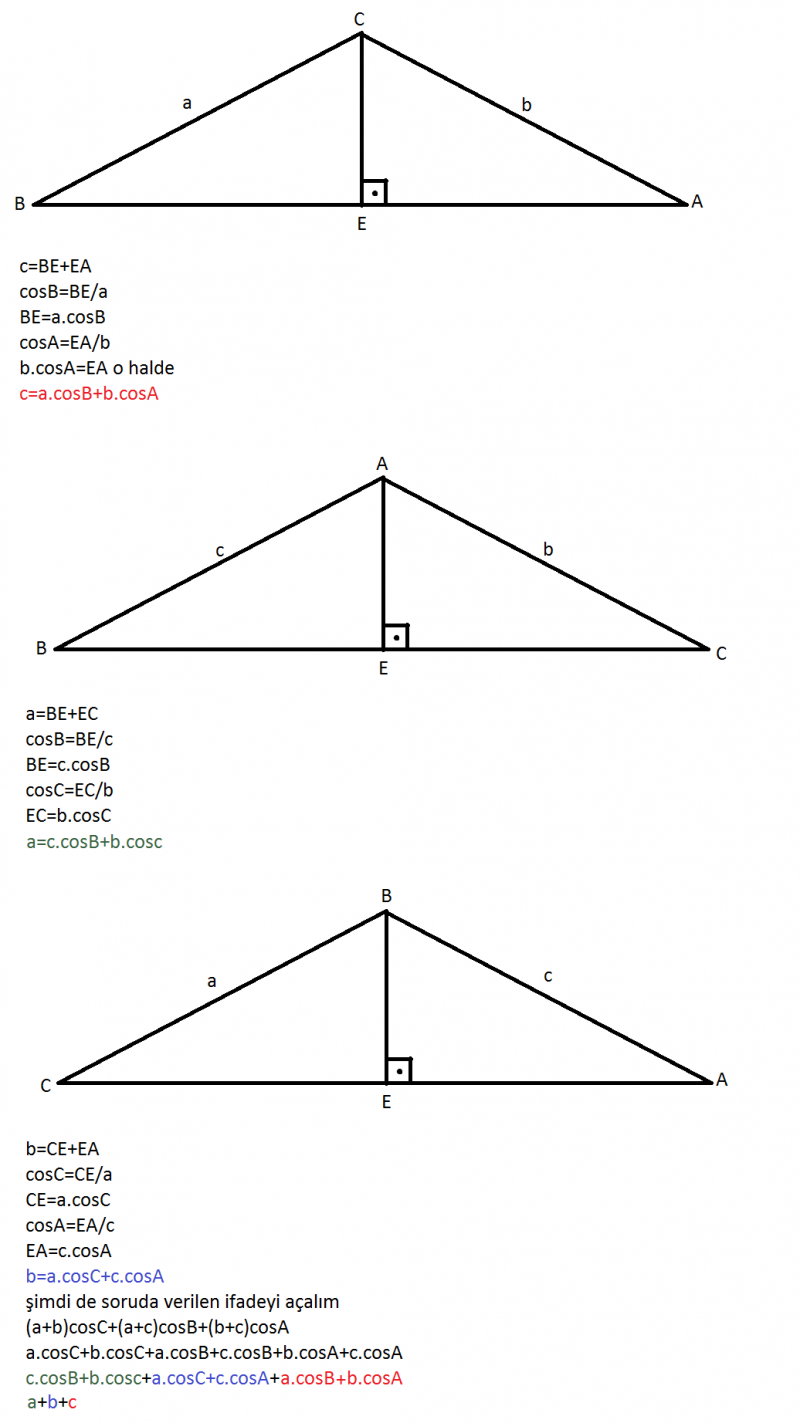
Bir ABC üçgeninde A,B,C açılarının karşılarındaki kenar uzunlukları sırasıyla a br,b br ve c br dir.

buna göre, (a+b)cosC+(a+c)cosB+(b+c)cosA toplamı hangisine eşittir?

cevap (a+b+c)

5.soru

sin2x=-2x/11 denkleminin reel sayılarda kaç farklı kökü vardır?

cevap 7

6.soru

(3∏/4'den ∏'ye kadar)∫4dx/(1-tanx) integralinin değeri kaçtır?

7. soru

f(x)=2^x ve g(x)=x+3 fonksiyonları veriliyor.

lim (x---->2)[(f ⁻¹og)(x)]=m olduğuna göre m gerçel sayısı aşağıdaki aralıkların hangisindedir?

A- (0,1)
B- (1,2)
C- (2,3)
D- (3,4)
E- (4,5)

7
[(f ⁻¹og)(x)] i yazalım:

f ters (x)=log2 tabanında x olur.
g(x) i buna bağlarsak aradığımız fonksiyon "log 2 tabanında (x+3)" olur.

x=2 için log2tabannında (5), (2,3) aralığında olur.

3
(cos3x+i.sin3x)=(cos2x-i.sin2x) tarzında düzenlenme sonrası ne yapılabilir?

ilk çözümün için çok teşekkür ederim. limit x=2 için denemeyi yapmamışım.

3.soruda zaten o kural çok açık görülüyor.ben köklerden birini eksik hesapladım o yüzden foruma sordum

ne demek,

kural mı hangi kural
diğer kökleri nasıl buldun acabâ?

1. soru c olabilir mi?

1.sorunun cevabı d seçeneği maalesef.

5) sinx=-2x/11 eşitliğinin x=0 da sağlandığı açıktır. Eğer bir x pozitif sayısı bu denklemi sağlarsa -x sayısı da bu denklemi sağlar. O yüzden biz sadece pozitifleri düşünelim. Bulduğumuz her pozitif kökün negatifi de bir kök olacaktır.

y=-2x/11 foksiyonunda pozitif x değerleri için y<0 olduğundan sinüs fonksiyonun minimum -1 değerini aldığı noktalara bakalım. x=3pi/2 için sinx=-1 dir. Dolayısıyla sinx fonksiyonunun grafiği (3pi/2, -1) noktasından geçer.

(0, 0) ve (3pi/2, -1) noktalarından geçen doğrunun eğimi -2/3pi dir. 3pi<11 olduğundan dördüncü bölgede y=-2x/11 doğrusu (0, 0) ve (3pi/2, -1) noktalarından geçen doğrunun üzerindedir. Yani y=-2x/11 doğrusu y=sinx eğrisini dördüncü bölgede en az iki noktada kesecektir. Daha fazla kesişim noktasının olmadığını aynı mantıkla gösterebilirsiniz.

Bulduğumuz dördüncü bölgedeki 2 kesişim noktasının apsislerinin negatifleri de verilen eşitliğin kökleri olacaktır. Yani toplamda verilen denklemin 5 tane gerçel kökü vardır.

Bir önceki mesajda y=sinx alarak çözüm yapmışım onu y=sin(2x) yapınca 7 yerine 9 kök olması gerekiyor. 7 kök olması için y=sin(2x) ve y=-2x/11 fonksiyonlarının teğet olması gerekir. Teğet oldukları noktanın apsisi a olursa (yani verilen eşitliğin bir kökü a olursa), o noktadaki eğimleri aynı olmalıdır. Yani 2cos(2a)=-2/11 ya da cos(2a)=-1/11 olmalıdır. Bunu sağlayan a değeri sin(2a)=-2a/11 denklemini sağlamaz.

Cevap anahtarı 7 diye verilmişse yanlıştır. 9 olması gerekir. Sanırım grafik çizen programlara grafik çizilmiş ve büyük bir ölçekle bakıldığı için birbirine yakın olan iki kök tek kök olarak kabul edilmiştir.