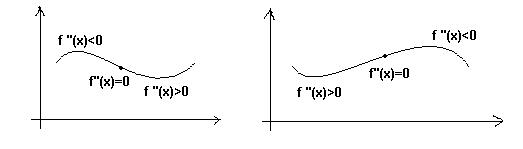2. Türev ve Büküm(Dönüm) Noktaları- Çukurluklar
A⊂R, f : A --> R, y=f(x) ; 1. ve 2. türevi olan bir fonksiyon olsun.
I) ∀x∈A için f ''(x)<0 ise, fonksiyonun grafiğinin çukurluk yönü aşağı doğrudur.
I) ∀x∈A için f ''(x)>0 ise, fonksiyonun grafiğinin çukurluk yönü yukarı doğrudur.
Fonksiyonun çukurluğunun, yön değiştirdiği nokta, dönüm(büküm) noktasıdır.
Dönüm noktasında, f ''(x)=0 dır.
Sonuçlar:
I) f(x) in grafiğindeki yerel ekstremum noktalarının apsisleri; f '(x) in grafiğinde , x eksenini kesen noktalardır.
II) f(x) in grafiğindeki dönüm noktalarının apsisleri; f ''(x) in grafiğinde, x eksenini kesen noktalardır.
III) f '(x) in grafiğindeki yerel ekstremum noktalarının apsisleri; f ''(x) in grafiğinde x eksenini kesen noktalardır.
IV) f(x) in grafiğindeki dönüm noktalarının apsisleri; f '(x) in grafiğinde , yerel ekstremum noktalarının apsisleridir.
Notlar:
I) f '(x0)=0 ve f ''(x0)=0 ise, x0 ekstremum nokta olmayabilir.
II) Dönüm noktasında, fonksiyonun 2. türevi tanımlı olmayabilir.
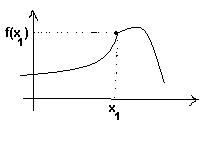
Bir noktada, ikinci türevin 0 olması , o noktanın dönüm noktası olmasını gerektirmez.
(x₁,f(x₁)) de; 2. türev tanımsız ama, dönüm noktasıdır.
III)Bir fonksiyonun bir noktada yerel ekstremumu olduğu halde, fonksiyon o noktada türevli olmayabilir.
IV) Fonksiyonun türevinin 0 olduğu noktada, türevin çift katlı kökü varsa; bu nokta, ekstremum nokta değildir.