1) f(x)=2x³-6x²+15 fonksiyonunun [-6,6] aralığında alabileceği en büyük değer kaçtır? (231)
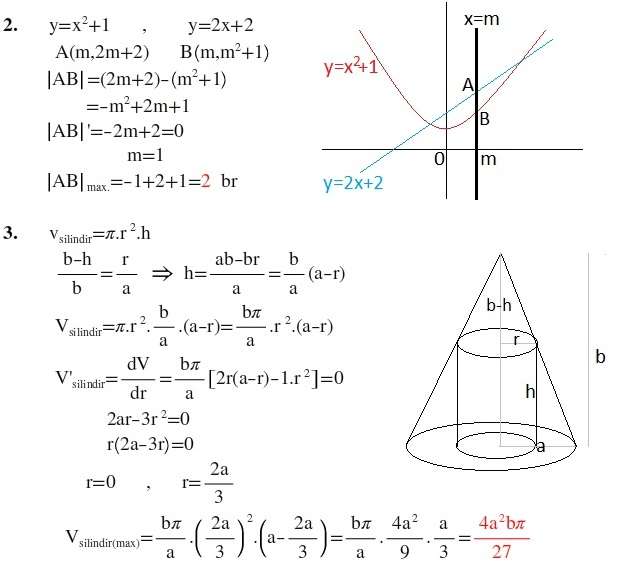
2) y=x²+1
y= 2x+2 fonksiyonlarının grafikleri üzerinde sırasıyla A ve B noktaları alınıyor. [AB], x=m doğrusu üzerinde, m reel sayısı da fonksiyonların kesim noktalarının apsisleri arasındadır.
A ile B noktaları birbirinden farklı old. göre |AB| uzunluğu en çok kaç birimdir? (2)
3) Taban yarıçapının uzunluğu a birim ve yüksekliği b birim olan dik koninin içine taban yarıçapının uzunluğu r olan dik silindir yerleştiriliyor.
Buna göre, en büyük hacimli silindirin hacminin a ve b türünden ifadesi nedir? (4/27∏a²b)
4) m pozitif reel sayı olmak üzere,
m üzeri m ifadesini en küçük yapan m sayısı kaçtır? (1/e)
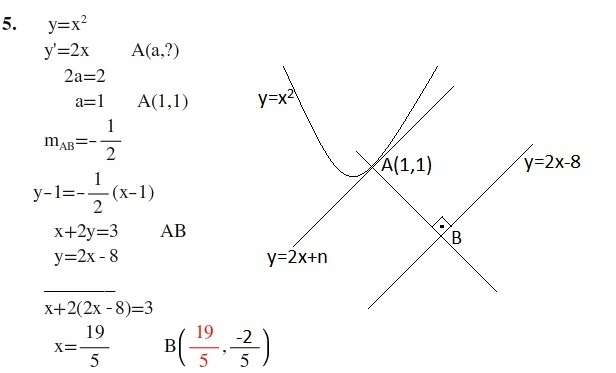
5) y=2x-8 doğrusunun y=x² parabolüne en yakın noktasının apsis değeri kaçtır? (19/5)
2) y=x²+1
y= 2x+2 fonksiyonlarının grafikleri üzerinde sırasıyla A ve B noktaları alınıyor. [AB], x=m doğrusu üzerinde, m reel sayısı da fonksiyonların kesim noktalarının apsisleri arasındadır.
A ile B noktaları birbirinden farklı old. göre |AB| uzunluğu en çok kaç birimdir? (2)
3) Taban yarıçapının uzunluğu a birim ve yüksekliği b birim olan dik koninin içine taban yarıçapının uzunluğu r olan dik silindir yerleştiriliyor.
Buna göre, en büyük hacimli silindirin hacminin a ve b türünden ifadesi nedir? (4/27∏a²b)
4) m pozitif reel sayı olmak üzere,
m üzeri m ifadesini en küçük yapan m sayısı kaçtır? (1/e)
5) y=2x-8 doğrusunun y=x² parabolüne en yakın noktasının apsis değeri kaçtır? (19/5)
f(x)=2x³-6x²+15 fonksiyonunun [-6,6] aralığında alabileceği en büyük değer kaçtır? (231)
f'(x)=6x²-12x=0 x1=0; x2=2
işaret tablosu yaparsak.;
.. (+) 0 (-) 2 (+) .. 2den sonrası artan fonksiyon. O halde max değer için x=6 koyalım. ( tanım aralığında)
f(6)=432 - 216 +15 = 231
f'(x)=6x²-12x=0 x1=0; x2=2
işaret tablosu yaparsak.;
.. (+) 0 (-) 2 (+) .. 2den sonrası artan fonksiyon. O halde max değer için x=6 koyalım. ( tanım aralığında)
f(6)=432 - 216 +15 = 231
4) m pozitif reel sayı olmak üzere,
m üzeri m ifadesini en küçük yapan m sayısı kaçtır? (1/e)
mm=y=f(m)olsun; türevini sıfıra eşitlersek değeri buluruz.
Önce doğal logaritmalarını alalım;
ln(mm)=lny
m.lnm=lny türev;
lnm+1=y'/y
y'=mm.(lnm+1) = 0
lnm=-1 m=1/e olur.
m üzeri m ifadesini en küçük yapan m sayısı kaçtır? (1/e)
mm=y=f(m)olsun; türevini sıfıra eşitlersek değeri buluruz.
Önce doğal logaritmalarını alalım;
ln(mm)=lny
m.lnm=lny türev;
lnm+1=y'/y
y'=mm.(lnm+1) = 0
lnm=-1 m=1/e olur.
Süleyman Oymak 16:48 13 May 2013 #4 
Çok teşekkür ederim.
Süleyman Oymak 22:56 13 May 2013 #6
Betulsvs, takıldığın sorulardan matematik ile iletişimin belli oluyor.
Bu sıra tam çalışılması gereken yerlere çalışıyorsun.
Başarı dileklerimle iyi çalışmalar.
Bu sıra tam çalışılması gereken yerlere çalışıyorsun.
Başarı dileklerimle iyi çalışmalar.
Elimden geleni yapmaya çalışıyorum hocam. Siz de çok yardımcı oluyorsunuz gerçekten çok teşekkür ederim tekrar.
Diğer çözümlü sorular alttadır.