duncanduncan 00:46 26 Ara 2010 #1
Q açısı 0 ile 45 arasında olmak üzere,z karmaşık sayısı için,
modül(z)=2
argüment(z)=Q
olduğuna göre,argüment(z+2) neye eşittir?açıklayabilirmisiniz(cvp Q/2)
başka bir soru z=(2011+2010i)/(2010-2011i)
olmak üzere,z karmaşık sayısının esas argümenti kaç derecedir?(i²=-1)açıklayabilirmisiniz (cevap 90)
modül(z)=2
argüment(z)=Q
olduğuna göre,argüment(z+2) neye eşittir?açıklayabilirmisiniz(cvp Q/2)
başka bir soru z=(2011+2010i)/(2010-2011i)
olmak üzere,z karmaşık sayısının esas argümenti kaç derecedir?(i²=-1)açıklayabilirmisiniz (cevap 90)
duncanduncan 01:21 26 Ara 2010 #2
acil yardım ederseniz sevinirim
MatematikciFM 01:24 26 Ara 2010 #3
Canım sorular üzerinde düşünüyorum ama biraz zor. Kolay tarafını bulamadım.
2. sorunun cevabı: paydanın eşleniği ile (2010+2011i)ile hem payı hem paydayı çarpın.sadeleştirme yapın.yalnızca i sayısı kalacaktır.argüment tanjantteta = b/a dan b=1 dir a=0 ona göre tanımsız olur.tanjant 90 derece vaya 270 derecede tanımsızdır yanız b nin işareti artı olduğu için argüment 90 derecedir. umarım işine yarar..matematikle kalın...
MatematikciFM 02:09 26 Ara 2010 #5
hayat ın cevabı doğru. Ben de eşlenikle çarptım ama birbirlerini ***üreceklerini düşünmediğimden sonuca gitmedim.
1. soru için sadece şunu bulabildim. Böyle bir eşitlik için, Q için 0-45 arası sınırlamak yanlış olur.Ancak 0-90 arası denilebilir. Kolaylık açısından Q=60 alınırsa z=1+kök3 olur. z+2 ise 3+kök3 Bunun da argümenti 30 derecedir. Denklemle yapılınca çözzümsüz gibi kalıyor. Ayrıca içimden bir ses bunun cevabının Q/2 değil, 90-Q olduğunu söylüyor. Şimdilik görebildiğim bu.
1. soru için sadece şunu bulabildim. Böyle bir eşitlik için, Q için 0-45 arası sınırlamak yanlış olur.Ancak 0-90 arası denilebilir. Kolaylık açısından Q=60 alınırsa z=1+kök3 olur. z+2 ise 3+kök3 Bunun da argümenti 30 derecedir. Denklemle yapılınca çözzümsüz gibi kalıyor. Ayrıca içimden bir ses bunun cevabının Q/2 değil, 90-Q olduğunu söylüyor. Şimdilik görebildiğim bu.
MatematikciFM 02:18 26 Ara 2010 #6
1. soru için t=2010 dönüşümü yapılırsa,
=((t+1)+t.i)/(t-(t+1).i
Payda t+(t+1).i ile çarpılırsa payda t^2+(t+1)^2 olur.
Pay için t+1)+t.i ile t+(t+1).i çarpılıp açıldığında, birbirini ***ürenler silindiğinde, (t^2+(t+1)^2).i kalıyor ve sadeleştirildiğinde i yalnız kalıyor. Gerisi hayat ın dediği gibi.
=((t+1)+t.i)/(t-(t+1).i
Payda t+(t+1).i ile çarpılırsa payda t^2+(t+1)^2 olur.
Pay için t+1)+t.i ile t+(t+1).i çarpılıp açıldığında, birbirini ***ürenler silindiğinde, (t^2+(t+1)^2).i kalıyor ve sadeleştirildiğinde i yalnız kalıyor. Gerisi hayat ın dediği gibi.
1.soru:z birin modulü verilmiş 2 dir.z ikininde modulü(z=2) onunda modulü 2 dir.karmaşık sayılarda moduller eşit olduğunda trigonometri kullanılan dönüşüm formüllerini uygulayabiliriz.yani toplamını bulabiliriz bu toplamda zaten birinin açısı Q tir diğerininde 0 derece.ordan dönüşümü kullandığında argümenti Q/2 olduğunu göreceksin.(bilgisayarda matematiksel işlemleri kullanmayı iyi bilemediğimden işleme dökemiyorum)dönüşüm formülleri cosA+cosB=2.cosA+B/2.cosA-B/2 ve sinA+sinB=2.sinA+B/2.cosA-B/2 A açısı=Q B açısı=0 derece alınacak..matematikle kalın...
1.soru:z birin modulü verilmiş 2 dir.z ikininde modulü(z=2) onunda modulü 2 dir.karmaşık sayılarda moduller eşit olduğunda trigonometri kullanılan dönüşüm formüllerini uygulayabiliriz.yani toplamını bulabiliriz bu toplamda zaten birinin açısı Q tir diğerininde 0 derece.ordan dönüşümü kullandığında argümenti Q/2 olduğunu göreceksin.(bilgisayarda matematiksel işlemleri kullanmayı iyi bilemediğimden işleme dökemiyorum)dönüşüm formülleri cosA+cosB=2.cosA+B/2.cosA-B/2 ve sinA+sinB=2.sinA+B/2.cosA-B/2 A açısı=Q B açısı=0 derece alınacak..matematikle kalın...
MatematikciFM 03:29 26 Ara 2010 #9
Teşekkürler hayat. Ne işle meşgulsünüz?
gereksizyorumcu 07:08 26 Ara 2010 #10
sorular cevaplanmış ama ben de 1. soru için farklı bir çözüm yazayım
şekilde görüldüğü gibi eklenen 2 sayısı reel eksene paraleldir ve uzunluğu da Z'nin uzunluğu kadardır dolayısıyla burada bir ikizkenar oluşur ve Z' sayısı reel eksenle θ/2 açısını yapmış olur.
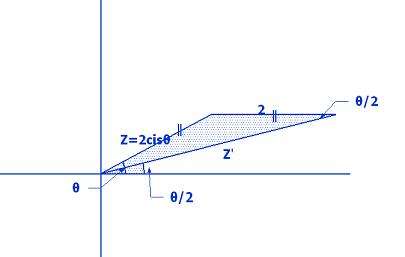
şekilde görüldüğü gibi eklenen 2 sayısı reel eksene paraleldir ve uzunluğu da Z'nin uzunluğu kadardır dolayısıyla burada bir ikizkenar oluşur ve Z' sayısı reel eksenle θ/2 açısını yapmış olur.
Diğer çözümlü sorular alttadır.