Çözümünü bilmediğim, uğraşıp da yapamadığım 3 soruyu sizlerle paylaşmak istiyorum.
1- 3 kişi, bir yerde buluşacaklar. Bu 3 kişiden her biri 60 dakikalık bir zaman diliminin herhangi bir dakikasında buluşma yerine gelip bekliyor ve 20 dakika sonra orayı terk ediyor.
Bu durumda 3 ünün de buluşma olasılığı nedir? (Bu soru üzerinde okuldaki zümreyle çok tartıştık ama herbirimiz farklı cevaplar bulduğu ve herbirimizin cevabı mantıken doğru gibi gözüktüğü için sonuca varamadık.)
2- 4 takımlı 2 torbadan çeyrek final karşılaşmalarının kurası çekilecektir. Kuradan önce, tüm eşleşmeleri bilebilme olasılığı nedir? (Bu soruyu, Fenerbahçenin Şampiyonlar liginde çeyrek final oynadığı zaman, kura çekiminden önce, televizyonda çıkan bir habere göre, adamın birinin, hangi takımın, hangi takımla oynayacağını tahmin etiğini duyan bir öğretmenimiz bize sormuştu. Biz de zümre olarak üzerinde çok kafa yorduk ama yine herbirimiz farklı cevaplar bulduk ve soruyu bıraktık.)
3- Bazı sitelerde buna benzer sorular var ama çözümünü hala bilmiyorum.
5 kişi gece bir köprüden geçecekler. Yanlarında bir fener var ve Köprü en fazla iki kişiyi taşıyabiliyor. Köprüden geçebilmeleri için de fenere ihtiyaçları var. 1. kişi köprüyü 12 dk da, 2. si 8 dakikada, 3. sü 6 dakikada, 4. 3 dakikada ve 5. si 1 dakikada köprüyü geçiyor. Fenerin ise 30 dakikalık yanam süresi var. Bu 5 kişiyi karşıya nasıl geçirirsiniz?
1- 3 kişi, bir yerde buluşacaklar. Bu 3 kişiden her biri 60 dakikalık bir zaman diliminin herhangi bir dakikasında buluşma yerine gelip bekliyor ve 20 dakika sonra orayı terk ediyor.
Bu durumda 3 ünün de buluşma olasılığı nedir? (Bu soru üzerinde okuldaki zümreyle çok tartıştık ama herbirimiz farklı cevaplar bulduğu ve herbirimizin cevabı mantıken doğru gibi gözüktüğü için sonuca varamadık.)
2- 4 takımlı 2 torbadan çeyrek final karşılaşmalarının kurası çekilecektir. Kuradan önce, tüm eşleşmeleri bilebilme olasılığı nedir? (Bu soruyu, Fenerbahçenin Şampiyonlar liginde çeyrek final oynadığı zaman, kura çekiminden önce, televizyonda çıkan bir habere göre, adamın birinin, hangi takımın, hangi takımla oynayacağını tahmin etiğini duyan bir öğretmenimiz bize sormuştu. Biz de zümre olarak üzerinde çok kafa yorduk ama yine herbirimiz farklı cevaplar bulduk ve soruyu bıraktık.)
3- Bazı sitelerde buna benzer sorular var ama çözümünü hala bilmiyorum.
5 kişi gece bir köprüden geçecekler. Yanlarında bir fener var ve Köprü en fazla iki kişiyi taşıyabiliyor. Köprüden geçebilmeleri için de fenere ihtiyaçları var. 1. kişi köprüyü 12 dk da, 2. si 8 dakikada, 3. sü 6 dakikada, 4. 3 dakikada ve 5. si 1 dakikada köprüyü geçiyor. Fenerin ise 30 dakikalık yanam süresi var. Bu 5 kişiyi karşıya nasıl geçirirsiniz?
Hocam 1. sorunuzun 2 kişilik 3 kişilik , 20 dakikalık ya da 30 dakikalık bekleme süresi olan versiyonlarını önceden görmüştüm ve çözmüştüm
sorunun bu haliyle cevabının 7/27 olması lazım.
2 kişilik durumdan başlayıp genel bir çözüm yazmaya çalışayım;
n=kişisayısı olsun=şu an 2
r=kişilerin bekleme zamanının tüm zamana oranı=şu an 20/60=1/3
2 kişi için şekil çizelim (3 kişi için çizmek biraz zor)

gri bölgenin alanının tüm alana oranı bize gereken şey , tüm alan zaten 1*1=1 olmasını biz ayarladık. gri bölgenin alanı hesaplansa yeterli
=r.1-kırmızı bölge
=r-r.r/2=r-r²/2
=1/3-1/18=5/18
şimdi bu sadece 1 kişi için , diğer kişi için de benzer bir buluşma alanı hesaplanabileceğinden bu bulduğumuz değeri 2 ile çarpmalıyız ve 2 kişi , 60dakikalıkdilimde 20 dakika bekleme süresiyle buluşma ihtimali 5/9 bulunur
buradan 3 ya da n kişiye geçiş yapalım;
n boyutta (gri+kırmızı) bölge taban alanı rn-1 olan bir prizmadır ve yüksekliği de 1 dir, toplam hacmi=rn-1
yine n boyutta kırmızı bölgeyse n boyutun tabanı rn-1 yüksekliği r olan prizmasının bizim birim kübüzümün içinde kalmayan kısımlarından oluşur.(şeklini çizebilsem daha güzel olacaktı ama yapabilirsem onu da sonra ekleyeyim)
bu kırmızı bölgenin hacmini de
rn-∫rx=0 xn-1dx=rn-rn/n bulunur.
bunu ilk bulduğumuz hacimden çıkarırsak
=rn-1-rn+rn/n
bu son değeri de kişi sayısıyla çarptığımızda tüm ihtimal
=n.rn-1-n.rn+rn bulunur.
burada sizin sorunuz için n=3 ve r=1/3 olduğundan
P=3.(1/3)²-3.(1/3)³+(1/3)³
=9/27-3/27+1/27=7/27 bulunuyor.
sorunun bu haliyle cevabının 7/27 olması lazım.
2 kişilik durumdan başlayıp genel bir çözüm yazmaya çalışayım;
n=kişisayısı olsun=şu an 2
r=kişilerin bekleme zamanının tüm zamana oranı=şu an 20/60=1/3
2 kişi için şekil çizelim (3 kişi için çizmek biraz zor)
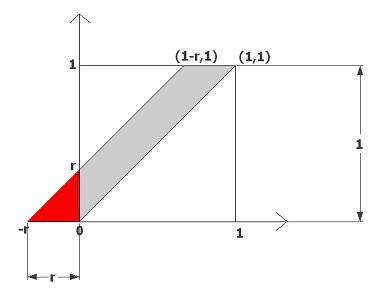
gri bölgenin alanının tüm alana oranı bize gereken şey , tüm alan zaten 1*1=1 olmasını biz ayarladık. gri bölgenin alanı hesaplansa yeterli
=r.1-kırmızı bölge
=r-r.r/2=r-r²/2
=1/3-1/18=5/18
şimdi bu sadece 1 kişi için , diğer kişi için de benzer bir buluşma alanı hesaplanabileceğinden bu bulduğumuz değeri 2 ile çarpmalıyız ve 2 kişi , 60dakikalıkdilimde 20 dakika bekleme süresiyle buluşma ihtimali 5/9 bulunur
buradan 3 ya da n kişiye geçiş yapalım;
n boyutta (gri+kırmızı) bölge taban alanı rn-1 olan bir prizmadır ve yüksekliği de 1 dir, toplam hacmi=rn-1
yine n boyutta kırmızı bölgeyse n boyutun tabanı rn-1 yüksekliği r olan prizmasının bizim birim kübüzümün içinde kalmayan kısımlarından oluşur.(şeklini çizebilsem daha güzel olacaktı ama yapabilirsem onu da sonra ekleyeyim)
bu kırmızı bölgenin hacmini de
rn-∫rx=0 xn-1dx=rn-rn/n bulunur.
bunu ilk bulduğumuz hacimden çıkarırsak
=rn-1-rn+rn/n
bu son değeri de kişi sayısıyla çarptığımızda tüm ihtimal
=n.rn-1-n.rn+rn bulunur.
burada sizin sorunuz için n=3 ve r=1/3 olduğundan
P=3.(1/3)²-3.(1/3)³+(1/3)³
=9/27-3/27+1/27=7/27 bulunuyor.
2. sorunuzu büyük ihtimalle çözebilirim, 3. sorunuz için de uğraşıp çözmeye çalışacağım ama onu çözüp çözemeyeceğimi bilemiyorum 
2. sorunuz için evsahipliği olma durumunu da bildiğini düşünmezsek (Fenerbahçe-Chelsea ile Chelsea-Fenerbahçe eşleşmesini aynı varsayıyorum) cevap 1/4! oluyor.
bu sonuca şöyle basit bir mantıkla varabiliriz;
kura çekme işlemini gözümüzün önüne getirelim
1. torbadan takımlar sırayla gelsinler ve rakiplerini diğer torbadan çeksinler. (bu işlemle tüm durumları ortaya koyabiliriz sanırım burada şüphemiz yok)
1. takım 4 takım seçebilir
sıradaki takıma 3 takım kalmıştır ve 3 ihtimal de onun için vardır
sıradaki için 2 ihtimal
son takım içinse tek ihtimal
sonuçta 4.3.2.1=24 ihtimal oluşabilir.
seçen takımların sıralamasının bir önemi yoktur çünkü oradan yeni bir ihtimal çıkmaz sadece varolan maçların numarası değişir örneğin Fenerbahçe-Chelsea maçı 2. maç değil de 4. maç olur gibi
tabi burada 1. torbanın her takımının 2. torbanın her takımıyla eşleşmesinin mümkün olduğunu varsayıyorum (yanlış hatırlamıyorsam çeyrek finalde aynı ülke takımları eşleşebiliyordu yani, burada da sorun yok)
eğer ev sahipliğini de katarsak toplam 24.4! eşleşme oluyor, ihtimal de 1/384 oluyor ki her iki durumda da televizyondaki kişinin bildiği şeyin ihtimali çok da düşük değil.
bu sonuca şöyle basit bir mantıkla varabiliriz;
kura çekme işlemini gözümüzün önüne getirelim
1. torbadan takımlar sırayla gelsinler ve rakiplerini diğer torbadan çeksinler. (bu işlemle tüm durumları ortaya koyabiliriz sanırım burada şüphemiz yok)
1. takım 4 takım seçebilir
sıradaki takıma 3 takım kalmıştır ve 3 ihtimal de onun için vardır
sıradaki için 2 ihtimal
son takım içinse tek ihtimal
sonuçta 4.3.2.1=24 ihtimal oluşabilir.
seçen takımların sıralamasının bir önemi yoktur çünkü oradan yeni bir ihtimal çıkmaz sadece varolan maçların numarası değişir örneğin Fenerbahçe-Chelsea maçı 2. maç değil de 4. maç olur gibi
tabi burada 1. torbanın her takımının 2. torbanın her takımıyla eşleşmesinin mümkün olduğunu varsayıyorum (yanlış hatırlamıyorsam çeyrek finalde aynı ülke takımları eşleşebiliyordu yani, burada da sorun yok)
eğer ev sahipliğini de katarsak toplam 24.4! eşleşme oluyor, ihtimal de 1/384 oluyor ki her iki durumda da televizyondaki kişinin bildiği şeyin ihtimali çok da düşük değil.
şöyle bi bakıyodum galiba 3. soruyu da çözdüm
(1,3,6,8,12)-----------------()
(6,8,12)---------------------(1,3) ...........(1ve3 geçer , 3dk., toplam 3 dk.)
(1,6,8,12)-------------------(3) .............(1 geri döner , 1dk. , toplam 4dk.)
(1,6)------------------------(3,8,12).......(8ve12 geçer , 12dk, toplam 16dk.)
(1,3,6)----------------------(8,12)..........(3geri döner , 3dk. , toplam 19dk.)
(3)--------------------------(1,6,8,12)....(1ve6 geçer , 6dk. , toplam 25dk.)
(1,3)------------------------(6,8,12).......(1geri döner , 1dk. , toplam 26dk.)
()---------------------------(1,3,6,8,12)..(1ve3 tekrar geçer , 3dk. , toplam 29dk.)
toplam 29 dakikada bile işlem bitebiliyor. 1dk. arttı artık onunla da feneri kim tutacak kavgası yaparlar
(1,3,6,8,12)-----------------()
(6,8,12)---------------------(1,3) ...........(1ve3 geçer , 3dk., toplam 3 dk.)
(1,6,8,12)-------------------(3) .............(1 geri döner , 1dk. , toplam 4dk.)
(1,6)------------------------(3,8,12).......(8ve12 geçer , 12dk, toplam 16dk.)
(1,3,6)----------------------(8,12)..........(3geri döner , 3dk. , toplam 19dk.)
(3)--------------------------(1,6,8,12)....(1ve6 geçer , 6dk. , toplam 25dk.)
(1,3)------------------------(6,8,12).......(1geri döner , 1dk. , toplam 26dk.)
()---------------------------(1,3,6,8,12)..(1ve3 tekrar geçer , 3dk. , toplam 29dk.)
toplam 29 dakikada bile işlem bitebiliyor. 1dk. arttı artık onunla da feneri kim tutacak kavgası yaparlar
Sayın gereksizyorumcu, öncelikle sorularıma kafa yorduğunuz ve çözdüğünüz için size teşekkür ederim.
3. sorudan başlıyim. Ben hep 1 dk da geçen kişiye feneri taşıtıyordum. Hiç böyle düşünmemiştim. Bu kurt-kuzu sorusunun benzeriymiş. Bu soru netleşti.
2. soru aslında çok basit gibi gözüküyor. Çözülemeyecek bir soru değilmiş. Ya biz çok karmaşık düşündük o yüzden sonuca varamadık ya da başka bir durum var. Öncelikle 1. ve 2. soruların çözümü için uzun zamandır uğraşmadım, Şimdilik de uğraşmak istemiyorum Sadece forumdakilerin fikirlerini öğrenmek istiyorum Daha sonra müsait bir zamanda iyice kafa yorup soruları netleştiricem.
1. soruya gelince, Sizin yaptığınız çözümün benzerini o zaman bir öğretmen daha yapmıştı. Ama o zaman da kafama yatmamıştı 2 nedenden dolayı. 1. si, bu zamana kadar ben hiçbir olasılık sorusunun alan ya da hacimle çözüldüğünü görmedim, duymadım. Çözümünüz bir taraftan mantıklı ama öbür taraftan niye özel olarak bu soruda alan veya hacim hesabı yapılıyor kafama yatmadı. Ayrıca bir A olayının olasılığı s(A)/s(E) olduğu için olasılık hesabının yapılabilmesi için öncelikle örnek uzayın belirlenmesi gerekmiyor mu? Bu soru için kimse net bir örnek uzay belirleyemedi. Bir de size bir öğretmenimizin yaptığı bir yorumu söyleyeyim. Demişti ki, bu soru zamandan bağımsızdır. Yani 60 dakikada 20 dakika beklemekle, 60 günde 20 gün beklemenin hiçbir farkı yok. Cevap direk 1/3 tür. Ne diyorsunuz?
3. sorudan başlıyim. Ben hep 1 dk da geçen kişiye feneri taşıtıyordum. Hiç böyle düşünmemiştim. Bu kurt-kuzu sorusunun benzeriymiş. Bu soru netleşti.
2. soru aslında çok basit gibi gözüküyor. Çözülemeyecek bir soru değilmiş. Ya biz çok karmaşık düşündük o yüzden sonuca varamadık ya da başka bir durum var. Öncelikle 1. ve 2. soruların çözümü için uzun zamandır uğraşmadım, Şimdilik de uğraşmak istemiyorum Sadece forumdakilerin fikirlerini öğrenmek istiyorum Daha sonra müsait bir zamanda iyice kafa yorup soruları netleştiricem.
1. soruya gelince, Sizin yaptığınız çözümün benzerini o zaman bir öğretmen daha yapmıştı. Ama o zaman da kafama yatmamıştı 2 nedenden dolayı. 1. si, bu zamana kadar ben hiçbir olasılık sorusunun alan ya da hacimle çözüldüğünü görmedim, duymadım. Çözümünüz bir taraftan mantıklı ama öbür taraftan niye özel olarak bu soruda alan veya hacim hesabı yapılıyor kafama yatmadı. Ayrıca bir A olayının olasılığı s(A)/s(E) olduğu için olasılık hesabının yapılabilmesi için öncelikle örnek uzayın belirlenmesi gerekmiyor mu? Bu soru için kimse net bir örnek uzay belirleyemedi. Bir de size bir öğretmenimizin yaptığı bir yorumu söyleyeyim. Demişti ki, bu soru zamandan bağımsızdır. Yani 60 dakikada 20 dakika beklemekle, 60 günde 20 gün beklemenin hiçbir farkı yok. Cevap direk 1/3 tür. Ne diyorsunuz?
esas ben teşekkür ederim bu güzel sorular için
olasılık sorularının alanla çözülmesi sadece geometrik bir kolaylık olması açısından
oradaki tüm olası bölge örnek uzayı temzil ediyor , yukarıdaki şekil için 1x1 lik birim kare , 3 boyut için 1x1x1 lik birim küp vs. (tabi bazen olası bölge kare ya da küp olmaz sorunun koşullarına göre bir çekidüzen verilir, mesele değişkenlerin değişim aralığının uzayda kapladığı yeri belirlemek)
hocamızın 60 günlük dilimde 20 gün bekleyip gitme yorumu ise bu soruyla aynı olması açısından evet bu souyla ihtimali anı ama bu ihtimalin 1/3 olması yorumu nereden geliyor onu da ben anlamdım çünkü 60 günü 1440*60 dakikaya bölüp sadece bu dakikalar üzerinde geliş işlemlerinin oranını 1/1440*60 olarak varsayıp hesap yapılsa cevap 7/27 ye çok yakın bir değer çıkıyor.
yani sorunun cevabını simülasyon yardımıyla da test ettim. 10000 tane 0-60 aralığında random number seçtirip bunlardan en büyüğüyle en küçüğü arasındaki farkın 20 den (ya da belirleyeceğiniz herhangi bir sayıdan) çok olmadığı durumlarını sayınca yaklaşık olarak 2600 tanesini falan bu durumu sağladığını görüyoruz. 26/100 de zaten 7/27 ye oldukça yakın. sorunun cevabından şüphem yok sadece daha şık ve güzel çözümleri var mıdır orasını merak ediyorum. bence daha kısa ve kolay anlaşılır bir çözümü de vardır.
olasılık sorularının alanla çözülmesi sadece geometrik bir kolaylık olması açısından
oradaki tüm olası bölge örnek uzayı temzil ediyor , yukarıdaki şekil için 1x1 lik birim kare , 3 boyut için 1x1x1 lik birim küp vs. (tabi bazen olası bölge kare ya da küp olmaz sorunun koşullarına göre bir çekidüzen verilir, mesele değişkenlerin değişim aralığının uzayda kapladığı yeri belirlemek)
hocamızın 60 günlük dilimde 20 gün bekleyip gitme yorumu ise bu soruyla aynı olması açısından evet bu souyla ihtimali anı ama bu ihtimalin 1/3 olması yorumu nereden geliyor onu da ben anlamdım çünkü 60 günü 1440*60 dakikaya bölüp sadece bu dakikalar üzerinde geliş işlemlerinin oranını 1/1440*60 olarak varsayıp hesap yapılsa cevap 7/27 ye çok yakın bir değer çıkıyor.
yani sorunun cevabını simülasyon yardımıyla da test ettim. 10000 tane 0-60 aralığında random number seçtirip bunlardan en büyüğüyle en küçüğü arasındaki farkın 20 den (ya da belirleyeceğiniz herhangi bir sayıdan) çok olmadığı durumlarını sayınca yaklaşık olarak 2600 tanesini falan bu durumu sağladığını görüyoruz. 26/100 de zaten 7/27 ye oldukça yakın. sorunun cevabından şüphem yok sadece daha şık ve güzel çözümleri var mıdır orasını merak ediyorum. bence daha kısa ve kolay anlaşılır bir çözümü de vardır.
Sayın gereksizyorumcu, 1/3 cevabı benim de kafama yatmadı zaten. Sizin çözümünüzün de tam olarak yanlış olduğunu söylemedim. Sizin de söylediğiniz gibi başka bir çözüm, özellikle, olasılık kavramlarının açık açık kullanıldığı bir çözüm üretilinceye kadar, bu çözümü, yok sayıyorum. Bu benim için sadece alternatif çözüm kapsamına girer. Esas çözüm, örnek uzayın aslının kullanıldığı çözümdür benim için.
