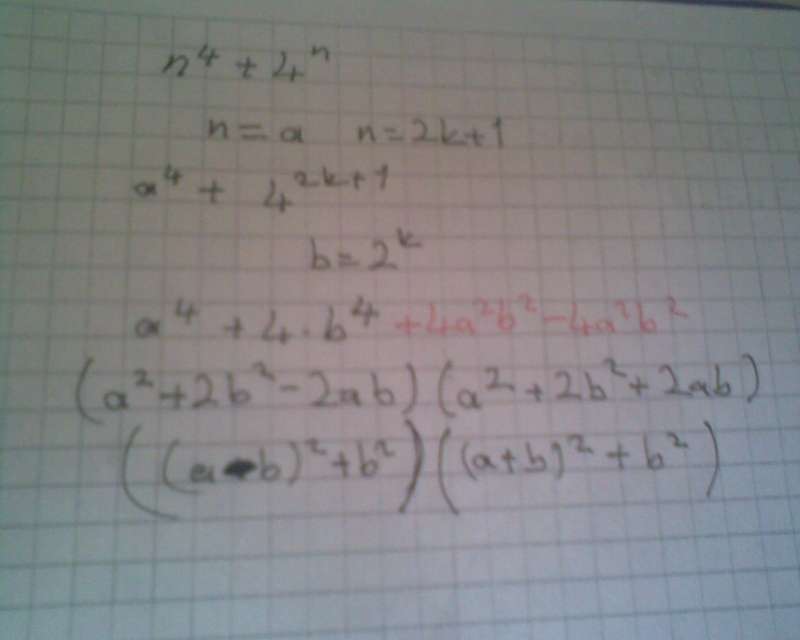liselere yönelik yarışma sorularıymış merak ettim çözümleri sorayım dedim
1) Eğer n, 1 den büyük bir tamsayı ise n⁴+4n sayısının asal olmayacağını gösteriniz.
2)a,b ve c sayıları birbirinden farklı reel sayılar olsunlar.
³√a-b+³√b-c+³√c-a=0 olamayacağını gösteriniz.