liselere yönelik yarışma sorularıymış merak ettim çözümleri sorayım dedim
1) Eğer n, 1 den büyük bir tamsayı ise n⁴+4n sayısının asal olmayacağını gösteriniz.
2)a,b ve c sayıları birbirinden farklı reel sayılar olsunlar.
³√a-b+³√b-c+³√c-a=0 olamayacağını gösteriniz.
1) Eğer n, 1 den büyük bir tamsayı ise n⁴+4n sayısının asal olmayacağını gösteriniz.
2)a,b ve c sayıları birbirinden farklı reel sayılar olsunlar.
³√a-b+³√b-c+³√c-a=0 olamayacağını gösteriniz.
ben ufak yol göstermeler yapayım çözemezseniz ya da çözüm yapılmazsa akşam bilgisayardan yazmaya çalışırım.
1.
n için çiftlik ve teklik durumlarını inceleriz
n=2k ise sorun yoktur
n=2k+1 ise
a=n ve b=2^k için sayımız a^4+4.b^4 olur
buna da 4a²b² ekleyip çıkartıp çarpanlarına ayırabilirsiniz, sonuçta oluşan parçaların da 1 den büyüklüğünü ispatlarsanız işlem tamamlanır.
2.
genelliği bozmadan a<b<c dersiniz
negatif olanların içerisini de ters çevirip diğer tarafa atarsınız.
sonra da b-a=x, c-b=y ve c-a=x+y diyip ili tarafın küpünü alırsanız çıkacaktır.
1.
n için çiftlik ve teklik durumlarını inceleriz
n=2k ise sorun yoktur
n=2k+1 ise
a=n ve b=2^k için sayımız a^4+4.b^4 olur
buna da 4a²b² ekleyip çıkartıp çarpanlarına ayırabilirsiniz, sonuçta oluşan parçaların da 1 den büyüklüğünü ispatlarsanız işlem tamamlanır.
2.
genelliği bozmadan a<b<c dersiniz
negatif olanların içerisini de ters çevirip diğer tarafa atarsınız.
sonra da b-a=x, c-b=y ve c-a=x+y diyip ili tarafın küpünü alırsanız çıkacaktır.
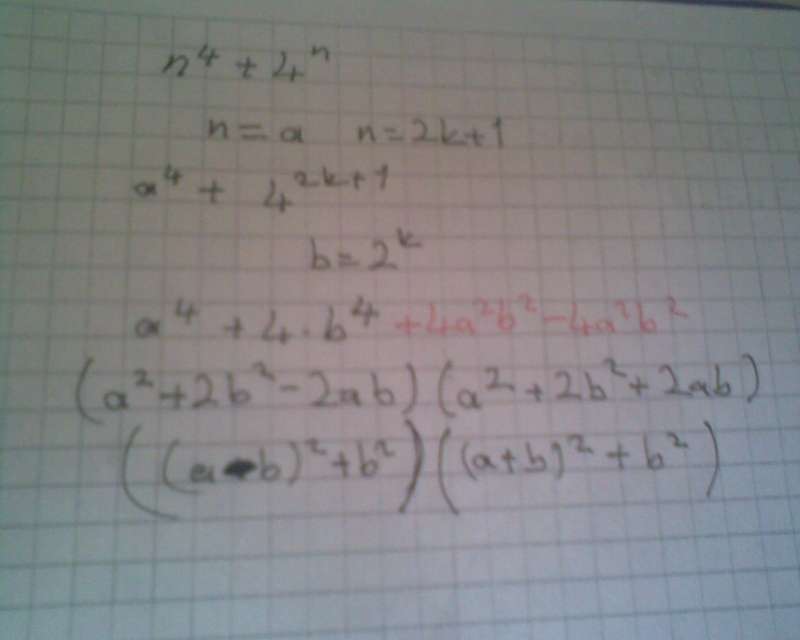
işlemin sonunda gelen her iki çarpanda 1 den büyük olacağı için asal olamazlar. Doğru mu hocam çözüm
ikinci soruda da dediğinizi yaptım kontrol ederseniz sevinirim hocam
³√c-a=³√b-a+³√c-b
³√x+y=³√x+³√y
her iki tarafın küpünü alınca
0= ³√x².³√y+³√x.³√y²
bu da hiç bir zaman sağlanmaz ispatlanmış olur böylece
³√c-a=³√b-a+³√c-b
³√x+y=³√x+³√y
her iki tarafın küpünü alınca
0= ³√x².³√y+³√x.³√y²
bu da hiç bir zaman sağlanmaz ispatlanmış olur böylece
ilk soruda bulduğunuz iki çarpanın da birden büyük olduğunu göstermeniz gerekir. Ya da çaranlardan birinin (küçük olanın) 1 olması durumunda verilenlerle bir çelişki elde ederseniz çözüm tamamlanır.
ikinci soruda bulduğunuz eşitlik bazı durumlarda sağlanır. O durumların mutlaka çelişki vereceğini bulursanız çözüm tamamlanmış olur. Bu arada x, y, z yerlerine onların küplerini alırsanız işlemleriniz biraz daha kolaylaşır.
ikinci soruda bulduğunuz eşitlik bazı durumlarda sağlanır. O durumların mutlaka çelişki vereceğini bulursanız çözüm tamamlanmış olur. Bu arada x, y, z yerlerine onların küplerini alırsanız işlemleriniz biraz daha kolaylaşır.
Çözümleri yazmıştım ama siteye resim yüklenmiyor şu ân.
Kabaca yazayım:
1. için n çift ise ifade daima 4 e bölünür. Tek sayı için;
2n22n ile toplayıp çıkarıp çarpanlara ayrıldığında n>1 için çarpanların hiçbiri 1 olmaz, 1 den büyük olur. Böylece bileşik sayı elde edilir ve ispat biter.
2.
a-b=x3
b-c=y3
c-a=z3 ve ifade=0 olsun x3+y3+z3=0 ve x+y+z=0 olur.
x3+y3+z3=(x+y+z)3-3(x+y)(x+z)(y+z)
xyz=0 olur ki x=0 (y veya z) ise a=b elde edilir ki bu çelişkidir. Demek ki kabulümüz yanlıştır. İfade=0 olamaz.
Kabaca yazayım:
1. için n çift ise ifade daima 4 e bölünür. Tek sayı için;
2n22n ile toplayıp çıkarıp çarpanlara ayrıldığında n>1 için çarpanların hiçbiri 1 olmaz, 1 den büyük olur. Böylece bileşik sayı elde edilir ve ispat biter.
2.
a-b=x3
b-c=y3
c-a=z3 ve ifade=0 olsun x3+y3+z3=0 ve x+y+z=0 olur.
x3+y3+z3=(x+y+z)3-3(x+y)(x+z)(y+z)
xyz=0 olur ki x=0 (y veya z) ise a=b elde edilir ki bu çelişkidir. Demek ki kabulümüz yanlıştır. İfade=0 olamaz.
Şİmdi denedim hocam yüklemeye başlamış.
Şİmdi denedim hocam yüklemeye başlamış.
tamam anladım çok teşekkürler
