euler formülü ve de moivre formülünün ispatlarını istiyorum

bunun mu?
yoksa

bunu mu ispatı?
İlki özdeşliği ikincisi formülü diye geçerde.
Aslında sormak istediği eiπ+1=0 ise Hocamızın verdiği formülden bu özdeşliğe ulaşabiliriz.
 ise
ise

olur.
Aslında bu formül muazzam bi formüldür.Pozitif bir sayının üssünü -1 e eşitleyen bir formüldür.Bu nasıl olur diye düşünmemeliyiz.Çünkü reel eksende işlem yapmıyoruz burada.
Aynı şekilde ln(-1)=iπ olur. Burdada tanımlı olamaz diyemeyiz.
 ise
ise 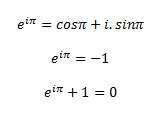
olur.
Aslında bu formül muazzam bi formüldür.Pozitif bir sayının üssünü -1 e eşitleyen bir formüldür.Bu nasıl olur diye düşünmemeliyiz.Çünkü reel eksende işlem yapmıyoruz burada.
Aynı şekilde ln(-1)=iπ olur. Burdada tanımlı olamaz diyemeyiz.
de moivre için ise şöyle bir şey buldum,



euler formülünden,

 (de moivre formülü)
(de moivre formülü)


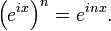
euler formülünden,

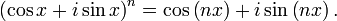 (de moivre formülü)
(de moivre formülü)
i sayısının x e göre bir sabit olmasından hareketle
(cosx-isinx)eix ifadesinin x e göre türevini alalım
=(cosx-isinx)'.eix+(cosx-isinx).(eix)'
=(-sinx-icosx).eix+(cosx-isinx).i.eix
=eix.(-sinx-icosx+icosx-i²sinx)
=eix.(-sinx-icosx+icosx+sinx)
=0
bu ifadenin türevi sıfırmış yani sabit fonksiyonmuş yani her x değeri için aynı değeri alıyormuş
x=0 için değeri 1 olduğuna göre
(cosx-isinx)eix=1 her zaman sağlanmalıdır.
eşitliği (cosx-isinx)'in eşleniği olan (cosx+isinx) ile çarparsak
(cos²x-i²sin²x)eix=cosx+isinx
(cos²x+sin²x)eix=cosx+isinx , her x için (cos²x+sin²x)=1 olduğundan
eix=cosx+isinx=cisx olur.
(cosx-isinx)eix ifadesinin x e göre türevini alalım
=(cosx-isinx)'.eix+(cosx-isinx).(eix)'
=(-sinx-icosx).eix+(cosx-isinx).i.eix
=eix.(-sinx-icosx+icosx-i²sinx)
=eix.(-sinx-icosx+icosx+sinx)
=0
bu ifadenin türevi sıfırmış yani sabit fonksiyonmuş yani her x değeri için aynı değeri alıyormuş
x=0 için değeri 1 olduğuna göre
(cosx-isinx)eix=1 her zaman sağlanmalıdır.
eşitliği (cosx-isinx)'in eşleniği olan (cosx+isinx) ile çarparsak
(cos²x-i²sin²x)eix=cosx+isinx
(cos²x+sin²x)eix=cosx+isinx , her x için (cos²x+sin²x)=1 olduğundan
eix=cosx+isinx=cisx olur.
i sayısının x e göre bir sabit olmasından hareketle
(cosx-isinx)eix ifadesinin x e göre türevini alalım
=(cosx-isinx)'.eix+(cosx-isinx).(eix)'
=(-sinx-icosx).eix+(cosx-isinx).i.eix
=eix.(-sinx-icosx+icosx-i²sinx)
=eix.(-sinx-icosx+icosx+sinx)
=0
bu ifadenin türevi sıfırmış yani sabit fonksiyonmuş yani her x değeri için aynı değeri alıyormuş
x=0 için değeri 1 olduğuna göre
(cosx-isinx)eix=1 her zaman sağlanmalıdır.
eşitliği (cosx-isinx)'in eşleniği olan (cosx+isinx) ile çarparsak
(cos²x-i²sin²x)eix=cosx+isinx
(cos²x+sin²x)eix=cosx+isinx , her x için (cos²x+sin²x)=1 olduğundan
eix=cosx+isinx=cisx olur.
(cosx-isinx)eix ifadesinin x e göre türevini alalım
=(cosx-isinx)'.eix+(cosx-isinx).(eix)'
=(-sinx-icosx).eix+(cosx-isinx).i.eix
=eix.(-sinx-icosx+icosx-i²sinx)
=eix.(-sinx-icosx+icosx+sinx)
=0
bu ifadenin türevi sıfırmış yani sabit fonksiyonmuş yani her x değeri için aynı değeri alıyormuş
x=0 için değeri 1 olduğuna göre
(cosx-isinx)eix=1 her zaman sağlanmalıdır.
eşitliği (cosx-isinx)'in eşleniği olan (cosx+isinx) ile çarparsak
(cos²x-i²sin²x)eix=cosx+isinx
(cos²x+sin²x)eix=cosx+isinx , her x için (cos²x+sin²x)=1 olduğundan
eix=cosx+isinx=cisx olur.
konu için biraz geç olduğunun farkındayım ama yeni bir başlık açmayayım dedim
ex = x⁰/0!+x¹/1!+x²/2!+x³/3!... + xn/n! + .. olduğunu e sayısının tanımından biliyoruz
eğer cos ve sin fonksiyonlarının taylor seri açılımınlarını alırsanız
cosx=1-x²/2!+x⁴/4!..=(-1)n 2n/(2n)!+++
sinx =x-x³/3!+..+(-1)n x2n+1/(2n+1)!+...
ve
in = için
n = 4k = 1
n = 4k+1 = i
n= 4k+2 =-1
n = 4k+3 = -i oldugunu biliyoruz(k 0,+sonsuza kadar bütün reel sayılar)
o halde
eix yazarsak şu açılımı elde ederiz
eix= 1+ix-x²/2!...
yukarıdaki sinx ve cosx tanımlamalarımızı ele alırsak
eix = 1-x²/2!+x⁴/4!..+(-1)n 2n/(2n)!+.. + i*(x-x³/3!+..+(-1)n x2n+1/(2n+1)!...
olacagını görebiliriz
ki buda
eix = cosx+isinx i getirir.
ex = x⁰/0!+x¹/1!+x²/2!+x³/3!... + xn/n! + .. olduğunu e sayısının tanımından biliyoruz
eğer cos ve sin fonksiyonlarının taylor seri açılımınlarını alırsanız
cosx=1-x²/2!+x⁴/4!..=(-1)n 2n/(2n)!+++
sinx =x-x³/3!+..+(-1)n x2n+1/(2n+1)!+...
ve
in = için
n = 4k = 1
n = 4k+1 = i
n= 4k+2 =-1
n = 4k+3 = -i oldugunu biliyoruz(k 0,+sonsuza kadar bütün reel sayılar)
o halde
eix yazarsak şu açılımı elde ederiz
eix= 1+ix-x²/2!...
yukarıdaki sinx ve cosx tanımlamalarımızı ele alırsak
eix = 1-x²/2!+x⁴/4!..+(-1)n 2n/(2n)!+.. + i*(x-x³/3!+..+(-1)n x2n+1/(2n+1)!...
olacagını görebiliriz
ki buda
eix = cosx+isinx i getirir.
Diğer çözümlü sorular alttadır.
