Bugün dünyada bilişim teknolojisine dayalı hızlı bir değişim süreci yaşanmaktadır. Bu teknoloji, insan düşünce gücünü etkileyerek sistematik bilgiye güç katan bir dönemi beraberinde getirmiştir. Aslında bilişim teknolojisi; sistematik bilgiye dayalı, insana özgü alt davranışları ve yetenekleri kazandırma çabalarına yönelik yazılımlarla işlerlik kazanan bilgisayar ve iletişim alt yapılarından oluşur.
İçinde yaşadığımız yüzyılda matematik, geometri ve algoritmalar; problem çözmede, kavramsal anlamada ve anlamlandırmada yapısalcı yaklaşımlar matematik eğitimini dramatik biçimde değiştirmiştir. Bu değişim sürecinin hızlanmasında bilişim teknolojileri çok önemli rol oynamaktadır.
Bilgisayar donanımı, yazılımı ve iletişiminden oluşan bilişim teknolojisinin kendi içinde hızla gelişmesi, bilimsel yaklaşımları, eğitim ve öğretimdeki yeni yaklaşımları ve tüm sektörleri doğrudan etkileyerek uygulamaya yönelik yeni tekniklerin oluşturulup gelişmesine neden olmaktadır. Kısaca zihinsel üretkenliğinin öneminin arttığı bir dönemi beraberinde getirmiştir.
Bilgisayar destekli matematik öğretiminde, bilgisayarlar bir seçenek değil, sistemi tamamlayıcı bir rol üstlenmektedir.
Bu yöntem bilgisayarın, bir öğretim aracı ve öğretmen rehberliğinde interaktif çalışmalarla öğrenmenin meydana geldiği bir ortam olarak kullanılması esasına dayanır. Burada öğretmen, öğrenci çalışmalarını gözler ve keşfetme tekniklerine göre onları yönlendirir. Sınıfta, öğrenciler ne yaptıklarının farkında olmadan sık sık hata yapabilirler. İnteraktif yaklaşım sürecinde öğretmen rehberliği, öğrencilerin hatalarını düzeltmelerini kolaylaştırır, böyle bir ortamdaki öğrencilerin uygulama ve deneyimleri keşfetmeye dayalı becerilerini geliştirir.
Genel olarak keşfetme etkinlikleri, öğretmen rehberliğinde yapılmalıdır. Öğretmen, öğrenmeyi kolaylaştıracak etkin materyaller hazırlamalıdır. Hazırlanan materyaller; bilgisayar destekli öğretimin yapısalcı yaklaşım esaslarına göre düzenlenmiş bir içeriğe sahip olmalıdır.
Bilgisayar destekli öğretim; yazılım, donanım, öğretmen eğitimi, laboratuvar ve yardımcı personel eğitimi gibi temel bileşenlerden oluşur. Bu bileşenlerden her biri bilgisayar destekli öğretimde önemli rol oynar.
Bilgisayar Destekli Matematik Öğrenme ve Öğretmede Temel Ögeler
Bilgisayar, giriş bilgilerine bağlı olarak istenen sonuç bilgilerini üreten bir makinedir. Bilgisayarların, insan denetiminde, belleme, karar verme, hesaplama, görselleştirme ve kayıt tutma gibi üstün nitelikleri vardır. Ancak, fizil sel yapısı ile düşünüldüğünde kendi başına yetenekleri çok fazla fakat işlerliği olmayan bir makinedir. Bilgisayarların üstün nitelikleri ancak programlandığında ortaya çıkar.
Bir bilgisayar, donanım ve yazılımla işlerlik kazanır. Bilgisayar sisteminin elektronik ve mekanik parçalarına topluca bilgisayar donanımı denir. Bilgisayar donanımına işlerlik kazandıran programlar, çözümlemeler, programlama dilleri, derleyiciler ve işletim sistemleri topluca bilgisayar yazılımı olarak adlandırılır.
Kuralların tanımı, bilgisayarın yapmasını istediğimiz işlemlere göre değişeceğini göstermektedir. Bu nedenle bilgisayarlar, yaptıracağımız işe dayalı tanımlayacağımız matematiksel kurallarda (algoritmanın kurulmasında) biz insanlara, sınırsız özgürlük vermektedir. Yeter ki bu kuralları tanımlama becerilerini kazanmış olalım ve kuralları sistematik bilgi biçiminde ifade edebilelim. Kuralları tanımlama matematik öğretiminde etkin rol oynadığı unutulmamalıdır.
Bir problemin çözümü için gerekli olan sonlu sayıdaki işlemleri adım adım komutlarla sembolik olarak belli bir mantıksal sırada tanımlayan düzene ya da hesaplama yöntemine algoritma denir.
Algoritmalar, “Başla” komutu ile başlar “Dur” komutu ile noktalanır. Aslında, algoritma bir sistematik bilgidir. Bir probleme ait matematiksel modelin çözümü için kullanılabilecek algoritmalar arasında birinin seçimi için çeşitli nedenler öne sürülebilir. Ancak, algoritmanın hızı (işlemlerde olduğu zaman) ve elde edilen sonuçlar algoritmanın seçimini etkileyen en önemli iki faktördür. Görevleri aynı olan algoritmalar arasında seçim yapılırken hızlı olan algoritma tercih edilir.
İnsanlar, bilgisayarlarla programlama dilleri aracılığı ile iletişim kurarlar. Bu nedenle, programlama dilleri matematiksel olarak tanımlanabilen dillerdir. Pascal, C, Prolog ve benzerleri birer programlama dilidir. Programlama dilleri, bilgisayarlara bir işin nasıl yapılacağını aktaran kurallar içerir. Program, bir problemi çözmek ya da öğrenmek için gerekli işlemlerin saptanması ve tanımlaması ile işlemlerin sırasının belirlenmesi olarak ifade edilebilir. Diğer bir şekli ile verilen bir problemi çözmek ya da öğrenmek için kurulacak bir algoritmanın, bir programlama dilinde kodlanmış biçimine program denir. Üst seviyedeki programlara yazılım denir.
İşletim sistemi, bilgisayarların çevre birimleri ve dış dünya ile iletişimini sağlayan üst düzeydeki yazılımlardır.
Yazılan programın bilgisayara yüklenip işlerlik kazanabilmesi için o programlama dilinin derleyicisi, bilgisayara yüklenmiş olmalıdır. Aksi durumda, o programlama dilinde kodlanmış program bilgisayarda çalıştırılamaz.
Program bilgisayara yüklendikten sonra, önce derleme işlemi yapılır. Eğer derleme hatası yoksa bilgisayardan sonuç alınır. Aksi durumda, derleme hatası düzeltildikten sonra tekrar aynı program denenir. Derleyiciler, kodlanan programı bilgisayarda makine diline dönüştürür. Makine diline çevrilmiş program, bilgisayarın fizik sel birimlerini programdaki komutlara göre harekete geçirerek işlem yapmasını sağlar ve beklenen sonuçları üretir.
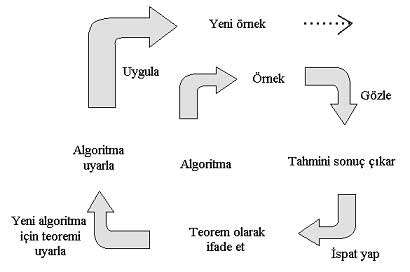
Program (yazılım) geliştirme, bir problemin bilgisayarda çözümü ya da öğretimi için, insan düşüncesi ve buluşçu yaklaşıma dayalı olarak, gerekli olan komutların, belli bir mantık yapısı içinde ifade edilmesine dayanır. Bu süreç üç aşamadan oluşur: