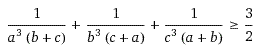1.(IMO1960-S2)
eşitsizliğinin sağlandığı tüm x∈R değerlerini bulunuz.
2.(IMO1961-S2)
Kenar uzunlukları a,b,c ve alanı S olan her üçgende
a2+b2+c2≥4S√3
eşitsizliğinin sağlandığını gösteriniz.
Hangi durumlarda eşitlik olur?
3.(IMO1964-S2)
a,b, ve c bir üçgenin kenar uzunluklarıyken
a2(b+c-a)+b2(a+c-b)+c2(a+b-c)≤3abc
olduğunu gösteriniz.
4.(IMO1984-S1)
x,y,z negatif olmayan reel sayılar ve x+y+z=1 ise
0 ≤ xy+yz+zx-2xyz ≤7/27
olduğunu gösteriniz.
5.(IMO1995-S2)
a,b,c ∈ R+ ve abc=1 ise
olduğunu gösteriniz.
uğraşmak isteyenleri düşünerek çözümlerini ileri bir tarihe bırakalım.