gereksizyorumcu 11:58 17 Ara 2010 #1 1.(IMO1960-S2)
eşitsizliğinin sağlandığı tüm x∈R değerlerini bulunuz.
2.(IMO1961-S2)
Kenar uzunlukları a,b,c ve alanı S olan her üçgende
a2+b2+c2≥4S√3
eşitsizliğinin sağlandığını gösteriniz.
Hangi durumlarda eşitlik olur?
3.(IMO1964-S2)
a,b, ve c bir üçgenin kenar uzunluklarıyken
a2(b+c-a)+b2(a+c-b)+c2(a+b-c)≤3abc
olduğunu gösteriniz.
4.(IMO1984-S1)
x,y,z negatif olmayan reel sayılar ve x+y+z=1 ise
0 ≤ xy+yz+zx-2xyz ≤7/27
olduğunu gösteriniz.
5.(IMO1995-S2)
a,b,c ∈ R+ ve abc=1 ise
olduğunu gösteriniz.
uğraşmak isteyenleri düşünerek çözümlerini ileri bir tarihe bırakalım.
eşitsizliğinin sağlandığı tüm x∈R değerlerini bulunuz.
2.(IMO1961-S2)
Kenar uzunlukları a,b,c ve alanı S olan her üçgende
a2+b2+c2≥4S√3
eşitsizliğinin sağlandığını gösteriniz.
Hangi durumlarda eşitlik olur?
3.(IMO1964-S2)
a,b, ve c bir üçgenin kenar uzunluklarıyken
a2(b+c-a)+b2(a+c-b)+c2(a+b-c)≤3abc
olduğunu gösteriniz.
4.(IMO1984-S1)
x,y,z negatif olmayan reel sayılar ve x+y+z=1 ise
0 ≤ xy+yz+zx-2xyz ≤7/27
olduğunu gösteriniz.
5.(IMO1995-S2)
a,b,c ∈ R+ ve abc=1 ise
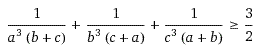
olduğunu gösteriniz.
uğraşmak isteyenleri düşünerek çözümlerini ileri bir tarihe bırakalım.
1.soru cevap küme ?
cevap boş kümemi yazacaktım sry
1.soru için x pozitif reel sayı ve x küçüktür 45 ∕8
gereksizyorumcu 18:33 01 Oca 2011 #5
x<45/8 kısmı doğru ama sol tarafının da karekökün içinin negatif olamaması ve paydanın 0 olamaması gibi nedenlerle
-1/2≤x ve x≠0 şeklinde olması lazım
-1/2≤x ve x≠0 şeklinde olması lazım
4. SORU: x,y,z negatif olmayan reel sayılar ve x+y+z=1 ise 0 ≤ xy+yz+zx-2xyz ≤7/27 olduğunu gösteriniz.
xy+yz+zx-2xyz=A diyelim.
önce 0 ≤A olduğunu sonrada A ≤7/27 olduğunu göstereceğim.
x+y+z=1 olduğundan bu üç sayıdan en az biri 1/2 den küçük olmalıdır üçü birden 1/2 ye eşit veya büyük olamaz.
xy+yz+zx-2xyz=x(y+z)+(1-2x)yz sağ tarafın 0 dan büyük olduğu kesinlikle gözüküyor.o halde 0 ≤A tamam.
x+y+z=1 ise y+z=1-x olduğunu ve aritmetik-geometrik ortalama eşitsizliğinide kullanarak A=xy+yz+zx-2xyz=x(y+z)+(1-2x)yz
≤x(1-x)+(1-2x)((y+z) ∕2)2
=x(1-x)+(1-2x)((1-x) ∕2)2
= 1/4(1+ x²-2 x³) .................(1)
parantez içindeki x²-2 x³ ifadesine tekrar AGO eşitsizliği kullandım
x²-2 x³=x.x(1-2x)
≤((x+x+1-2x)/3)3=1/27
bu durumu .............(1) nolu eşitlikte yerine yazarsak
A ≤1/4(1+1/27)=7/27
A ≤7/27 olduğunu gösterdik
NOT: her zaman geometrik ortalama ≤ aritmetik ortalama yazılabilir
örneğin a.b ≤((a+b)/2)2 yada a.b.c ≤((a+b+c)/3)3
xy+yz+zx-2xyz=A diyelim.
önce 0 ≤A olduğunu sonrada A ≤7/27 olduğunu göstereceğim.
x+y+z=1 olduğundan bu üç sayıdan en az biri 1/2 den küçük olmalıdır üçü birden 1/2 ye eşit veya büyük olamaz.
xy+yz+zx-2xyz=x(y+z)+(1-2x)yz sağ tarafın 0 dan büyük olduğu kesinlikle gözüküyor.o halde 0 ≤A tamam.
x+y+z=1 ise y+z=1-x olduğunu ve aritmetik-geometrik ortalama eşitsizliğinide kullanarak A=xy+yz+zx-2xyz=x(y+z)+(1-2x)yz
≤x(1-x)+(1-2x)((y+z) ∕2)2
=x(1-x)+(1-2x)((1-x) ∕2)2
= 1/4(1+ x²-2 x³) .................(1)
parantez içindeki x²-2 x³ ifadesine tekrar AGO eşitsizliği kullandım
x²-2 x³=x.x(1-2x)
≤((x+x+1-2x)/3)3=1/27
bu durumu .............(1) nolu eşitlikte yerine yazarsak
A ≤1/4(1+1/27)=7/27
A ≤7/27 olduğunu gösterdik
NOT: her zaman geometrik ortalama ≤ aritmetik ortalama yazılabilir
örneğin a.b ≤((a+b)/2)2 yada a.b.c ≤((a+b+c)/3)3
gereksizyorumcu 23:51 10 Oca 2011 #7
hocam elinize sağlık güzel bir çözüm olmuş.
sentetikgeo 19:32 29 Haz 2013 #8
5)
Verilen toplama S diyelim Cauchy'den
S.(a(b+c)+b(a+c)+c(a+b))≥(1/a+1/b+1/c)²
abc=1 old. 1/a+1/b+1/c=ab+ac+bc
a(b+c)+b(a+c)+c(a+b)=2(ab+ac+bc)
yani S≥(ab+ac+bc)/2
AO-GO eşitsizliğinden ab+ac+bc≥3.∛a²b²c²=3
yani S≥3/2
Verilen toplama S diyelim Cauchy'den
S.(a(b+c)+b(a+c)+c(a+b))≥(1/a+1/b+1/c)²
abc=1 old. 1/a+1/b+1/c=ab+ac+bc
a(b+c)+b(a+c)+c(a+b)=2(ab+ac+bc)
yani S≥(ab+ac+bc)/2
AO-GO eşitsizliğinden ab+ac+bc≥3.∛a²b²c²=3
yani S≥3/2
sentetikgeo 20:59 29 Haz 2013 #9
3)
a,b,c nin üçgenin kenarları olmasına gerek yok.
parantezleri açınca a³+b³+c³+3abc≥a²b+a²c+b²a+b²c+c²a+c²b
oluyor bu da zaten schur eşitsizliğinden geliyor.
∑a(a-b)(a-c)≥0
a,b,c nin üçgenin kenarları olmasına gerek yok.
parantezleri açınca a³+b³+c³+3abc≥a²b+a²c+b²a+b²c+c²a+c²b
oluyor bu da zaten schur eşitsizliğinden geliyor.
∑a(a-b)(a-c)≥0
sentetikgeo 21:41 29 Haz 2013 #10
2)
Bu eşitsizlik Weitzenböck eşitsizliği.
Heron formülünden
S=(1/4)√(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=(1/4)√2(a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴)
a²+b²+c²≥4S√3
<=>(a²+b²+c²)².(1/3)≥(4S)²=2(a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴)
<=>(1/3)[(a⁴+b⁴+c⁴)+2a²b²+2a²c²+2b²c²]≥2(a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴)
<=>a⁴+b⁴+c⁴≥a²b²+a²c²+b²c²
<=>(a²-b²)²+(a²-c²)²+(b²-c²)²≥0
Eşitliğin sağlanması için a=b=c olmalı yani üçgen eşkenar olmalı.
Bu eşitsizlik Weitzenböck eşitsizliği.
Heron formülünden
S=(1/4)√(a+b+c)(a+b-c)(a-b+c)(-a+b+c)=(1/4)√2(a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴)
a²+b²+c²≥4S√3
<=>(a²+b²+c²)².(1/3)≥(4S)²=2(a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴)
<=>(1/3)[(a⁴+b⁴+c⁴)+2a²b²+2a²c²+2b²c²]≥2(a²b²+a²c²+b²c²)-(a⁴+b⁴+c⁴)
<=>a⁴+b⁴+c⁴≥a²b²+a²c²+b²c²
<=>(a²-b²)²+(a²-c²)²+(b²-c²)²≥0
Eşitliğin sağlanması için a=b=c olmalı yani üçgen eşkenar olmalı.
Diğer çözümlü sorular alttadır.