1)

2)
6.1321=x (mod23) x kaçtır?
Arkadaşlar burada uzatıp 13'ün 11.kuvvetine götürürsek 1'i elde ederiz ama benim burada sormak istediğim bunun bir kısa yolu var mıdır sınavda çıktığı için süreyi nasıl indirgeyebiliriz?
İlgilenen arkadaşlara teşekkürler
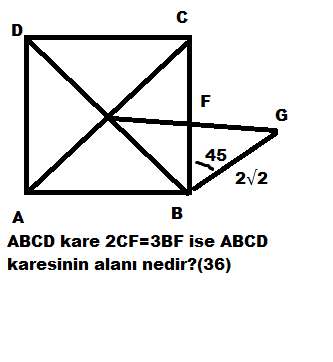
2)
6.1321=x (mod23) x kaçtır?
Arkadaşlar burada uzatıp 13'ün 11.kuvvetine götürürsek 1'i elde ederiz ama benim burada sormak istediğim bunun bir kısa yolu var mıdır sınavda çıktığı için süreyi nasıl indirgeyebiliriz?
İlgilenen arkadaşlara teşekkürler
2. soru için fermat teoremini kullanabilirsin
2.soru için şöyle düşünülebilir.
Fermat teoreminden 1322≡1(mod23) gelir.
6.1321≡(6.1322)/(13)≡ (mod23) burda 1322=1 olur
6.1322/13=6/13 gelir. paydadan 23 çıkar
6/13≡-6/10=-3/5 bu sefer pay kısmına 23 ekle
-3/5≡20/5≡4
Fermat teoreminden 1322≡1(mod23) gelir.
6.1321≡(6.1322)/(13)≡ (mod23) burda 1322=1 olur
6.1322/13=6/13 gelir. paydadan 23 çıkar
6/13≡-6/10=-3/5 bu sefer pay kısmına 23 ekle
-3/5≡20/5≡4
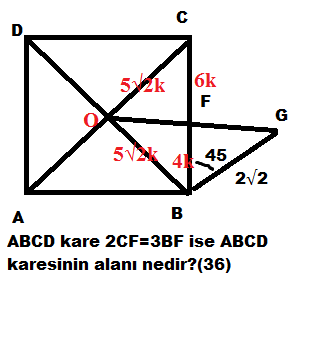
A(BFG)=4k.2√2.
1
√2
.
1
2
=4k
A(OBG)=5√2k.2√2/2=10k
A(OFB)=10k-4k=6k
|FB|=4k
|CF|=6k olduğundan A(OCF)=9k
A(BOC)=9k+6k=15k=5√2k.5√2k/2=25k²
25k²=15k
5k²=3k
k=3/5
A(ABCD)=4.15k=4.15.3/5=36
