https://img201.imageshack.us/img201/228/v697.jpg
https://img18.imageshack.us/img18/2230/gzvf.jpg
https://img850.imageshack.us/img850/4524/zqjp.jpg
https://img824.imageshack.us/img824/3844/v0d0.jpg
Yardımlarınız için şimdiden teşekkürler
https://img18.imageshack.us/img18/2230/gzvf.jpg
https://img850.imageshack.us/img850/4524/zqjp.jpg
https://img824.imageshack.us/img824/3844/v0d0.jpg
Yardımlarınız için şimdiden teşekkürler
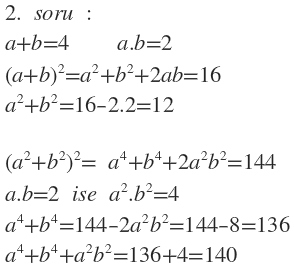
Tesekkurler
v697.jpg ile ilgili 7. soru cevabı:
x+√x=5
* √x=5-x olur.
Soruda 6x + x√x isteniyor.
=6x + x(5-x) (* burada √x yerine koyuyoruz)
=6x + 5x -x²
=11x -x² değerine de ulaşsak olur.
Bunun için bize verilen eşitliğin her iki tarafının da karesini alırız.
(x+ √x)²=5²
x² + 2x√x + x = 25
x ( x + 2√x ) + x =25
x ( x + 2 (5-x)) + x=25 (* burada √x yerine koyuyoruz)
x ( x + 10 -2x ) + x=25
x (-x +10) + x=25
-x² + 10x + x =25
-x² + 11x = 25
Böylece cevabı 25 olarak bulmuş oluruz.
x+√x=5
* √x=5-x olur.
Soruda 6x + x√x isteniyor.
=6x + x(5-x) (* burada √x yerine koyuyoruz)
=6x + 5x -x²
=11x -x² değerine de ulaşsak olur.
Bunun için bize verilen eşitliğin her iki tarafının da karesini alırız.
(x+ √x)²=5²
x² + 2x√x + x = 25
x ( x + 2√x ) + x =25
x ( x + 2 (5-x)) + x=25 (* burada √x yerine koyuyoruz)
x ( x + 10 -2x ) + x=25
x (-x +10) + x=25
-x² + 10x + x =25
-x² + 11x = 25
Böylece cevabı 25 olarak bulmuş oluruz.
1) İlk olarak ifadeyi;
216+1 = a / (22+1)(24+1)(28+1) şeklinde yazalım.
232-1 = (216+1)(216-1) olacağından ;
(216-1)a / (22+1)(24+1)(28+1) olmalıdır.
(216-1)=(22+1)(22-1)(24+1)(28+1) olacağından sadeleştirilmeler yapıldığında cevap 3a olarak bulunur.
(Not:Lütfen geometri soruları haricindeki sorularınızı şekille eklemeyin.Aksi takdirde bir dahaki sorularınızı çözemem.)
216+1 = a / (22+1)(24+1)(28+1) şeklinde yazalım.
232-1 = (216+1)(216-1) olacağından ;
(216-1)a / (22+1)(24+1)(28+1) olmalıdır.
(216-1)=(22+1)(22-1)(24+1)(28+1) olacağından sadeleştirilmeler yapıldığında cevap 3a olarak bulunur.
(Not:Lütfen geometri soruları haricindeki sorularınızı şekille eklemeyin.Aksi takdirde bir dahaki sorularınızı çözemem.)
3) ifadeyi ; x³-2x-1+2=0 biçiminde yazabiliriz.
Bu durumda; x³-1=2(x-1) ise (x-1)(x²+x+1)=2(x-1) den x²+x-1=0 ise
x²+x+5=6 olacaktır.
Bu durumda; x³-1=2(x-1) ise (x-1)(x²+x+1)=2(x-1) den x²+x-1=0 ise
x²+x+5=6 olacaktır.
4) x³+y³-x²y-xy²=0 ise ifadeyi;
(x+y)³=4x²y+4xy² = 4xy(x+y) biçiminde yazabiliriz. Buradan;
(x+y)² = 4xy = (x-y)²=0 ise x=y olarak bulunur.
(x+y)/(x-2y) oranı y yerine x yazarak;
2x/-x = -2 olarak bulunur.
(x+y)³=4x²y+4xy² = 4xy(x+y) biçiminde yazabiliriz. Buradan;
(x+y)² = 4xy = (x-y)²=0 ise x=y olarak bulunur.
(x+y)/(x-2y) oranı y yerine x yazarak;
2x/-x = -2 olarak bulunur.
zqjp.jpg ile ilgili 4. sorunun cevabı:
a² - 3a -5 =0 ise a² - (15/a) nedir diye soruluyor. Burada sorulan ifade:
=a² - (15/a) işlemine devam edersek,
(i) =(a³ -15)/a ifadesine ulaştığımızda küplü bir açılım içerdiğini görürüz. Bu nedenle, verilen ifadeyi a² - 3a -5 =0 x³+y³ = (x+y)(x²-xy+y²) şeklinde yazmaya çalışalım.
a² - 3a -5 +14=0+14
a² - 3a +9 =14
(a+3)(a² - 3a +9)=14(a+3) Her iki tarafıda a+3 ile çarptık.
a³+3³= 14a + 14.3
a³+27= 14a+42
a³-14a=42-27
a³-14a=15
a³-15=14a buluruz.
(i) 'de belirtilen ifade de bulduğumuz değeri yerine koyalım.
=(a³ -15)/a
=14a/a
=14 bulmuş oluruz.
a² - 3a -5 =0 ise a² - (15/a) nedir diye soruluyor. Burada sorulan ifade:
=a² - (15/a) işlemine devam edersek,
(i) =(a³ -15)/a ifadesine ulaştığımızda küplü bir açılım içerdiğini görürüz. Bu nedenle, verilen ifadeyi a² - 3a -5 =0 x³+y³ = (x+y)(x²-xy+y²) şeklinde yazmaya çalışalım.
a² - 3a -5 +14=0+14
a² - 3a +9 =14
(a+3)(a² - 3a +9)=14(a+3) Her iki tarafıda a+3 ile çarptık.
a³+3³= 14a + 14.3
a³+27= 14a+42
a³-14a=42-27
a³-14a=15
a³-15=14a buluruz.
(i) 'de belirtilen ifade de bulduğumuz değeri yerine koyalım.
=(a³ -15)/a
=14a/a
=14 bulmuş oluruz.
zqjp.jpg ile ilgili 3. sorunun cevabı:
x≠1 olmak üzere, x³-2x+1 =0 olduğuna göre x²+x+5 ifadesinin değeri nedir?
Verilen ifadede x³-2x+1 =0 küp açılımı söz konusu. Bu nedenle,
Bu ifadeyi x³-y³=(x-y)(x²+xy+yy²) ifadesine benzetmeye çalışalım.
x³-2x+1-1+1 =0 Eşitliğin sol tarafında -1+1 ilave ettik.
x³-1-2x+2 =0
x³-1 =2x-2
(x-1)(x²+x+1)=2x-2
(x-1)(x²+x+1)=2(x-1)
x²+x+1=2
x²+x=1 olur.
Soruda x²+x+5 ifadesinde bulduğumuz değeri yerine koyarsak, 1+5=6 olur.
x≠1 olmak üzere, x³-2x+1 =0 olduğuna göre x²+x+5 ifadesinin değeri nedir?
Verilen ifadede x³-2x+1 =0 küp açılımı söz konusu. Bu nedenle,
Bu ifadeyi x³-y³=(x-y)(x²+xy+yy²) ifadesine benzetmeye çalışalım.
x³-2x+1-1+1 =0 Eşitliğin sol tarafında -1+1 ilave ettik.
x³-1-2x+2 =0
x³-1 =2x-2
(x-1)(x²+x+1)=2x-2
(x-1)(x²+x+1)=2(x-1)
x²+x+1=2
x²+x=1 olur.
Soruda x²+x+5 ifadesinde bulduğumuz değeri yerine koyarsak, 1+5=6 olur.
v0d0.jpg ile ilgili 11. sorunun cevabı:
x≠-y olmak üzere x³+y³-x²y-xy²=0 olduğuna göre (x+y)/(x-2y) oranı kaçtır?
x³+y³-x²y-xy²=0
x³-xy²+y³-x²y=0
x(x²-y²)+y(y²-x²)=0
x(x²-y²)= -y(y²-x²)
x(x-y)(x+y)= -y(y-x)(y+x)
x(x-y)= -y(y-x)
x(x-y)= y(x-y)
x=y olur.
Bu eşitlikten yararlanarak, (x+y)/(x-2y) ifadesinde yerine koyarsak,
=(x+y)/(x-2y)
=(x+x)/(x-2x)
=2x/(-x)
= -2 bulunur.
x≠-y olmak üzere x³+y³-x²y-xy²=0 olduğuna göre (x+y)/(x-2y) oranı kaçtır?
x³+y³-x²y-xy²=0
x³-xy²+y³-x²y=0
x(x²-y²)+y(y²-x²)=0
x(x²-y²)= -y(y²-x²)
x(x-y)(x+y)= -y(y-x)(y+x)
x(x-y)= -y(y-x)
x(x-y)= y(x-y)
x=y olur.
Bu eşitlikten yararlanarak, (x+y)/(x-2y) ifadesinde yerine koyarsak,
=(x+y)/(x-2y)
=(x+x)/(x-2x)
=2x/(-x)
= -2 bulunur.
