Limit, Çarpanlara Ayırma, İkinci Dereceden Denklem

1)
(x-2)/[(√3x²-8)-2] = ?

Cevap 1/3.Türevle çözümünü yapabilir misiniz?

2)
(6-x)/x . ln(1+ 4x/3) limitinin değeri kaçtır? (8)

Sorunun çözümünde 1/x=y demiş.Değişken değiştirmeden nasıl yapabilirim?

3) x²-2y²+xy+x+5y-2 ifadesinin çarpanlarından biri nedir?(x-y+2)

4) x²+(a-2)x+b=0 denkleminin bir kökü 6,
x²+(b+2)x+c=0 denkleminin bir kökü -4 tür.
Bu denklemlerin diğer kökleri ortak olduğuna göre, 7(a+b+c) ifadesinin değeri kaçtır? (cevap:-26)

4)Denklemleri katsayılar ve kökler arasındaki bağıntıya göre düzenleyelim.

x²+(a-2)x+b=0
x²+(b+2)x+c=0

Ortak köklere y diyelim. Bu durumda 1. denklemden b=6y ; a=-y-4 eşitlikleri elde edilir.
2. denklemden b=2-y ; c=-4y eşitlikleri gelecektir.

iki denklemden b ler eşitlenirse; 6y=2-y den y=2/7 bulunur.

cevap: 7((-30+12-8)/7) den -26 bulunur.

3) x²+xy−2y² = (x-y)(x+2y) biçiminde yazalım. Geriye kalan x+5y-2 (x-y)(x+2y) nin bir çarpanına benzetilmeye çalışalım. Bunun için elimizdeki y değerlerini olabildiğince azaltmak için bir x i ekleme çıkarma yöntemiyle denkleme ekleyelim.
Bu durumda (x-y)(x+2y)+2x+4y-x-2+y = (x-y+2)(x+2y)-(x+y+2) = (x-y+2)(x+2y-1) eşitliği elde edilir. Bu durumda ifademizin çarpanları (x-y+2) ve (x+2y-1) dir.

(x-2)/[(√3x²-8)-2] ifadesinin 1. türevi

1/[ 6x/2(√3x²-8)]
2 yazalım x yerine
1/[12/4) = 1/3

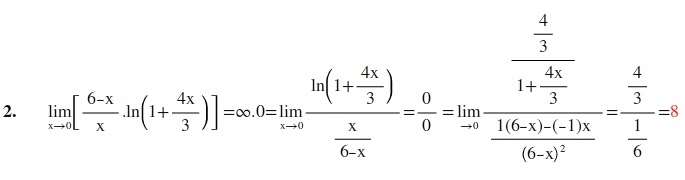
Herkese teşekkür ediyorum.

Hocam burada (6-x)/x'i logaritmanın üssü olarak yazıp değişken değiştirmeden 1 üssü sonsuz belirsizliğinden yapabilir miyiz?