Obeb Okek

1) y bir asal sayı olmak üzere, Recep misketlerini y li ve y+2 li gruplara ayırdığında her seferinde 5 misketi artıyor.

Recep'in 260 tan az misketi olduğu bilindiğine göre, en fazla kaç misketi olabilir? (257)


2)a ve b pozitif tamsayılardır.

4^a.5^b çarpımı 17 basamaklı en küçük doğal sayıyı belirttiğine göre a+b toplamı kaçtır? (24)


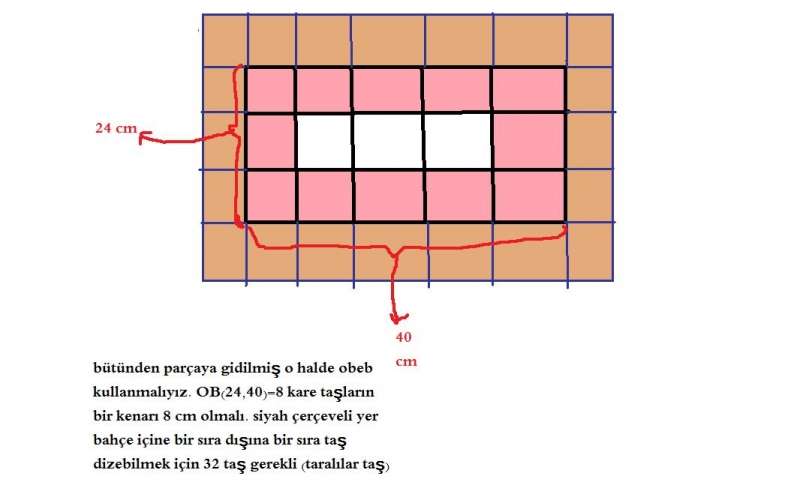
3)Boyutları 24 ve 40 metre olan dikdörtgen şeklindeki bir bahçenin çevresinde içeriden ve dışarıdan birer sıra kare taşlar döşenecektir.

Kare taşların alanı en büyük olacak şekilde bu iş için kaç kare taş gereklidir? (32)


4)OKEK(A,B) = 3.5²

koşuluna uyan kaç değişik (A,B) doğal sayı ikilisi vardır?(15)


5) x ve ye birer tamsayıdır.

(x-3)/y = x/(x+3)

olduğuna göre x in alabileceği pozitif değerlerin toplamı kaçtır? (10)

2)
17 basamaklı en küçük doğal sayı 10¹⁶'dır.
10¹⁶=2¹⁶.5¹⁶=4⁸.5¹⁶
8+16=24

4. soru takipte

4)burada kısa bir yol verilmişti sanırım (2a+1)(2b+1) formülü vardı

bunu uygularsak

(2.2+1)(2.1+1)=15

4)
A ve B 3 ve 5 çarpanlarından ulaşacaktır.

A=3^a.5^b
B=3^c.5^d

[A,B]=3.5² ise

max(a,c)=1 ve max(b,d)=2 olacak.
(a,c) ikilisi için (1,1),(1,0),(0,1) yani 3 farklı durum vardır.
(b,d) ikilisi için (2,0),(2,1),(0,2),(0,1),(2,2) yani 5 farklı durum vardır.

3.5=15

3) ebob(24,40)=8 demek ki kare taşlar 8 m^2 lik. Uzun kenarlara 40/8 den 5 er tane, kısa kenarlara ise 24/8 den 3 er tane olmak üzere toplam 16 taş döşenir. 2 sıra döşeneceği için de 16.2=32 taş olur.

3-

sağolun. 1.soruya bakabilecek varmı?

1) misket sayısı M olsun bize diyor ki y ve y+2 ye bölündüğünde kalan 5 tir
o zaman M-5 y ve y+2 ye tam bölünür
y ve y+2 ye bölünmesi demek ekoklarının da bölünmesi demektir
y ve y+2 aralarında asaldır ( Bir asal sayının 2 fazlası o asal sayıyla aralarında asaldır Örn. 3 ve 5 aralarında asal 2 ve 4 istisna)
burda y 5 ten büyük olmak zorunda çünkü y 5 ten küçük bir asal sayı olursa mesela 3 olursa kalan 5 olmaz kalan bölenden küçük olmalı o halde 5 ten büyük
y ve y+2 nin ekoku aralarında asal olduğundan çarpımlarına eşittir yani ekok(y,y+2)=y.(y+2)=y²+2y olur bu ekok M-5 i tam bölüyormuş bölüme K diyelim
M-5=(y²+2y).K+0
y 5 ten büyük demiştik ve asal sayı olacak y=7 için
M-5=63.K olur K=4 için
M-5=63.4=252 ---> M=257 olur
başkalarına da bakalım
y=11 için
M-5=143K olur K=1 için
M-5=143 ---> M=148 olur , K=2 için M-5=286 ---> M=291 olur 260 ı aşar
y=13 için
M-5=195K olur K=1 için
M-5=195 ---> M=200 olur , K=2 için M-5=390 ---> M=395 olur 260 ı aşar
y=17 için
M-5=323K olur zaten bu mümkün değildir
o halde en büyük değerimiz 257 dir

öğretmen olup sınavda sorsam böyle bir çözüm beklerdim ama bu sorunun özelinde tersten gitmek daha faydalı olabilir. (sonuçta bu bir test sorusu ve 60-70 saniye gibi bir sürede çözülmesi bekleniyor)

5 eksiği aralarındaki fark 2 olan 2 sayıya bölünen bir sayı arıyoruz (küçük bölen asal olacak)
259 sağlıyor mu? 254=2.127
258? 253=11.23
257? 252=2².3².7 , bu sayı 7 ve 9 a bölünüyor