f(x)=sin2x.cos2x f'(x)=?
f(x)=tan22x f'(∏/8)=?
f(x)=√sinx f'(∏/6)=?
f(x)=tan22x f'(∏/8)=?
f(x)=√sinx f'(∏/6)=?
C-1
(a.b)'=a'b+ab'
f(x)=sin2x.cos2x=>(sin2x)'cos2x+sin2x(cos2x)'
Zincir kuralını kullanmalıyız:
=(2.cos2x)cos2x+sin2x(2.-sin2x)=2cos²2x-2sin²2x
İyi günler.
f(x)=(tan(2x))²=tan2x.tan2x
tanx=sinx/cosx olduğundan bölüm kuralını* kullanırsak; ((sinx)'.(cosx)-(sinx)(cosx)')/(cos²x)=(cos²x+sin²x)/(cos²x)=1/(cos²x) olur.
(tan2x.tan2x)'=(tan2x)'(tan2x)+(tan2x)(tan2x)'
Zincir kuralını kullanalım:
(2/cos²2x)(tan2x)+(tan2x)(2/cos²2x)=4(tan2x)/(cos²2x)
İyi günler.
tanx=sinx/cosx olduğundan bölüm kuralını* kullanırsak; ((sinx)'.(cosx)-(sinx)(cosx)')/(cos²x)=(cos²x+sin²x)/(cos²x)=1/(cos²x) olur.
(tan2x.tan2x)'=(tan2x)'(tan2x)+(tan2x)(tan2x)'
Zincir kuralını kullanalım:
(2/cos²2x)(tan2x)+(tan2x)(2/cos²2x)=4(tan2x)/(cos²2x)
İyi günler.
C-3
f(x)=√sinx
Zincir kuralını kullanırsak;
(sinx)'.(√sinx)'=cosx.(1/(2√sinx))=(cosx)/(2√sinx) olur.
Az önceki çözümde bölüm kuralını yazmayı unutmuşum.
Bölüm Kuralı: (a/b)'=(a'b-ab')/b²
İyi günler.
kcancelik, 10. sınıf helâl olsun.
1)

2)

3)

1)
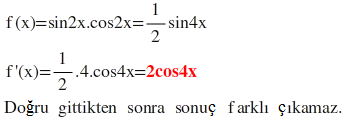
2)
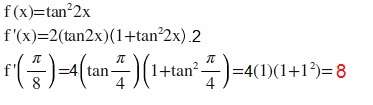
3)
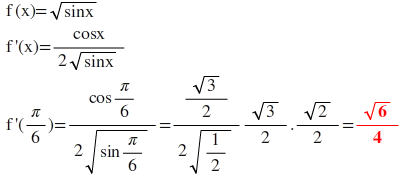
aynen bence de helal olsun... cevaplar için teşekkürler.
