1, cevap B.
2
3
Son soruyu şıklardan bulabildim, ama bir de çözümünü öğrenmeyi istedim.
4. kökü yrine yazıp polinom bölmesi yaptığımda sonucu 1 buluyorum
2
3
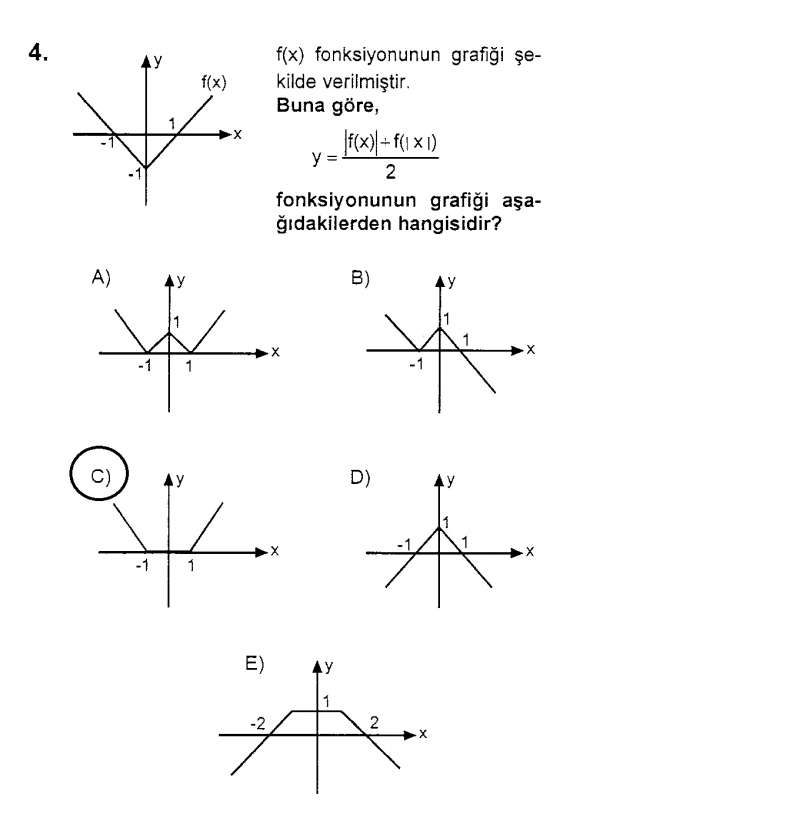
Son soruyu şıklardan bulabildim, ama bir de çözümünü öğrenmeyi istedim.
4. kökü yrine yazıp polinom bölmesi yaptığımda sonucu 1 buluyorum
C.1
Önce y≥|x|'e bakalım.
x>0 için;
|x|=0 olduğundan, y≥x olur. Bunun grafiğini çizmek için y=x doğrusunu çizer ve doğru dahil olmak üzere doğrunun üstünü tararız.
x=0 için;
y≥0 olur. Bunun grafiğinde de apsisi 0 ve ordinatı pozitif olan noktaları alırız.
x<0 için;
|x|=-x olduğundan y≥-x olur. Bunun grafiği için y=-x doğrusunu çizer ve doğru dahil olmak üzere doğrunun üstünü tararız.
Ve son olarak bu üç grafiği birleştirirsek şöyle olur:
Şimdi de |y-2|≤1'e bakalım. Bunu çözersek; 1≤y≤3 çıkar. (İsterseniz bunun nasıl geldiğini de anlatabilirim.) Grafiği de şöyledir:
Soruda sorulan ise; bu bağıntıların grafiklerinin sınırladıkları alan. Herhalde bu alanı da benzerlik yardımıyla bulabilirsiniz.(İsterseniz anlatabilirim.)
Kolay gelsin..
Önce y≥|x|'e bakalım.
x>0 için;
|x|=0 olduğundan, y≥x olur. Bunun grafiğini çizmek için y=x doğrusunu çizer ve doğru dahil olmak üzere doğrunun üstünü tararız.
x=0 için;
y≥0 olur. Bunun grafiğinde de apsisi 0 ve ordinatı pozitif olan noktaları alırız.
x<0 için;
|x|=-x olduğundan y≥-x olur. Bunun grafiği için y=-x doğrusunu çizer ve doğru dahil olmak üzere doğrunun üstünü tararız.
Ve son olarak bu üç grafiği birleştirirsek şöyle olur:
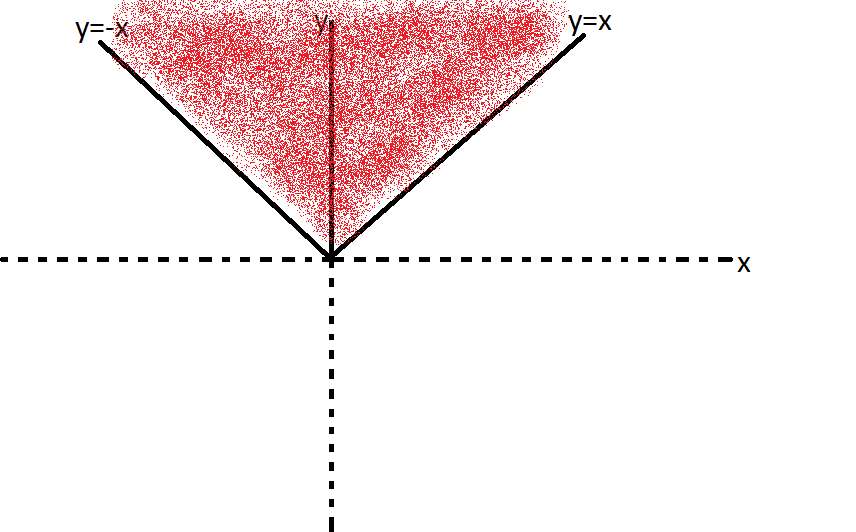
Şimdi de |y-2|≤1'e bakalım. Bunu çözersek; 1≤y≤3 çıkar. (İsterseniz bunun nasıl geldiğini de anlatabilirim.) Grafiği de şöyledir:
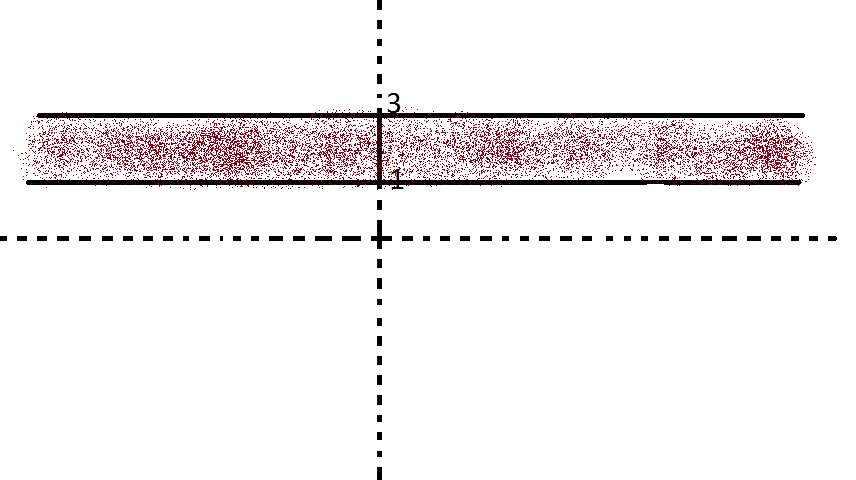
Soruda sorulan ise; bu bağıntıların grafiklerinin sınırladıkları alan. Herhalde bu alanı da benzerlik yardımıyla bulabilirsiniz.(İsterseniz anlatabilirim.)
Kolay gelsin..
C.2
İki tarafta da kökün derecesi(2) çift olduğu için iki taraf da mutlak değerle çıkar.
Yani; |x-3|=|y-4| olur.
Buradan iki sonuç çıkar:
1-) x-3=y-4 doğrusu bu durumu sağlar.
2-) x-3=-y+4 doğrusu bu durumu sağlar.
Bu durumu sağlayan iki doğru olduğuna göre; bu bağıntının grafiği de bu iki doğrudan oluşur. Yani şöyledir:
Bundan sonrası basit.(İA)
İki tarafta da kökün derecesi(2) çift olduğu için iki taraf da mutlak değerle çıkar.
Yani; |x-3|=|y-4| olur.
Buradan iki sonuç çıkar:
1-) x-3=y-4 doğrusu bu durumu sağlar.
2-) x-3=-y+4 doğrusu bu durumu sağlar.
Bu durumu sağlayan iki doğru olduğuna göre; bu bağıntının grafiği de bu iki doğrudan oluşur. Yani şöyledir:
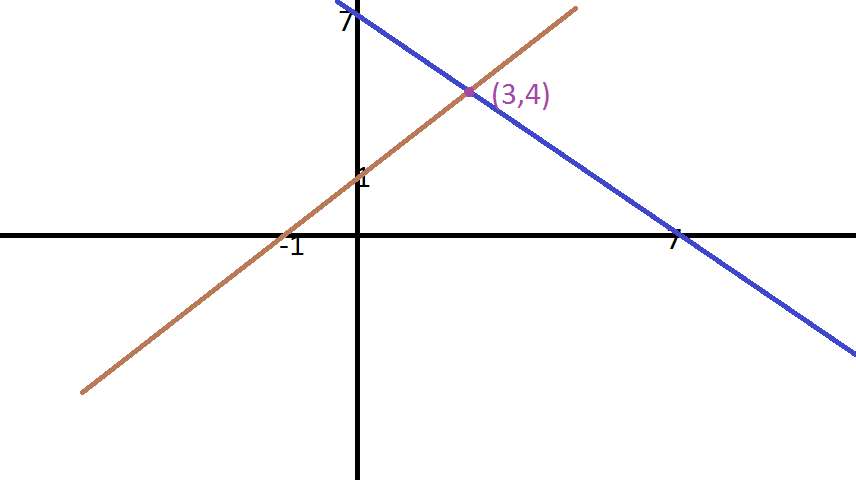
Bundan sonrası basit.(İA)
C.3
Öncelikle x>1 için bakalım.
|f(x)|=f(x) dir.
f(|x|)=f(x) dir. Dolayısıyla y=2f(x)/2=f(x) olur.
0≤x≤1 için;
|f(x)|=-f(x) dir.
f(|x|)=f(x) dir. Dolaysıyla y=0 olur.
-1≤x<0 için;
|f(x)|=-f(x) dir.
f(|x|)=f(-x)=f(x)'dir. Dolayısıyla y=0 olur.
x<-1 için;
|f(x)|=f(x)
f(|x|)=f(x) dir. Dolayısıyla y=f(x) olur.
Sonuçta C seçeneğindeki grafik çıkar.
Öncelikle x>1 için bakalım.
|f(x)|=f(x) dir.
f(|x|)=f(x) dir. Dolayısıyla y=2f(x)/2=f(x) olur.
0≤x≤1 için;
|f(x)|=-f(x) dir.
f(|x|)=f(x) dir. Dolaysıyla y=0 olur.
-1≤x<0 için;
|f(x)|=-f(x) dir.
f(|x|)=f(-x)=f(x)'dir. Dolayısıyla y=0 olur.
x<-1 için;
|f(x)|=f(x)
f(|x|)=f(x) dir. Dolayısıyla y=f(x) olur.
Sonuçta C seçeneğindeki grafik çıkar.
Limit için bir şey yapamıyorum. Beni aşıyor maalesef. 
gereksizyorumcu 23:41 13 Eki 2012 #6
limit sorusunda limitin olması için x→1 için üst tarafın da sıfır olması lazım
buradan k=3 bulunur , ister L'hospital uygularsınız ister bölme yaparsınız
sonuçta limit 0 bulunur.
buradan k=3 bulunur , ister L'hospital uygularsınız ister bölme yaparsınız
sonuçta limit 0 bulunur.
MatematikciFM 00:02 14 Eki 2012 #7
4)
polinom bölmesinde bölüm
x²+x-2
çıkıyor.
x=1 için limit 0 oluyor.
polinom bölmesinde bölüm
x²+x-2
çıkıyor.
x=1 için limit 0 oluyor.
MatematikciFM 00:04 14 Eki 2012 #8 limit sorusunda limitin olması için x→1 için üst tarafın da sıfır olması lazım
buradan k=3 bulunur , ister L'hospital uygularsınız ister bölme yaparsınız
sonuçta limit 0 bulunur.
buradan k=3 bulunur , ister L'hospital uygularsınız ister bölme yaparsınız
sonuçta limit 0 bulunur.
Emeklemeden koşmayı öğretmeyin öğrencilerimize.
Bu konuda hassasım biliyorsunuz
MatematikciFM 00:20 14 Eki 2012 #9
Örtmenim!, örtmenim !
Grafik soruları için, diycem var, diyebilir miyim ?
Grafik soruları için, diycem var, diyebilir miyim ?
Son Soru
Bu soruda payda 0 oluyor, dolayısıyla pay kısmı da 0 olmalı; yoksa limit tanımsız(∞) olur. Üst tarafın da 0 olması için x-1 çarpanı içermesi gerekir. Bu durumda x-1 ile tam bölünür. x=1 alırsak 1³-k+2=0 koşulu gelir, buradan k=3 çıkar.
Polinom bölmesi yaparsak bölüm x²+x-2 çıkar. Limit için x=1 alırsak 1+1-2=0 olur.
Fikri öğretmenim çözmüş zaten, bu akşam görememe sorunum var.
İyi günler.