karinca_52 19:52 21 Ağu 2012 #1
S1) İçinde 4 satı , 5 mavi bilye bulunan bir torbadan çekilen iki bilyeden birinin sarı olduğu biliniyor. Buna göre diğerinin mavi olma olasılığı kaçtır?
(cevap : 1/2)
S2) A torbasında 2 kırmızı , 6 mavi bilye , B torbasında 3 kırmızı ve 5 mavi bilye vardır.
iki torbadan da aynı anda çekilen birer bilyenin farklı renkde olma olasılığı kaçtır?
(cevap : 7 / 16)
S3) A torbasında 3 yeşil , 4 kırmızı B torbasında 2 yeşil , 5 kırmızı bilye vardır. Önce A torbasından bir bilye çekilip B torbasına atılıyor.sonra B torbasından bir bilye çekiliyor.
Buna göre B torbasından eşil bilye çekilmiş olma olasılığı kaçtır?
(cevap : 17/56)
S4) Bir torbada 4 sarı , 3 kırmızı ,2 bilye vardır. Torbadan aynı anda çekilen 3 bilyenin en az ikisinin aynı renkde olma olasılığı kaçtır?
(cevap : 5 / 7)
S5) ABCD bir dikdörtgen AB = 12 , BC = 5
ABCD dikdörtgeninde seçilen herhangi bir noktanın taralı bölgeye ait olmama olasılığı kaçtır?
(cevap : 1/2)
(cevap : 1/2)
S2) A torbasında 2 kırmızı , 6 mavi bilye , B torbasında 3 kırmızı ve 5 mavi bilye vardır.
iki torbadan da aynı anda çekilen birer bilyenin farklı renkde olma olasılığı kaçtır?
(cevap : 7 / 16)
S3) A torbasında 3 yeşil , 4 kırmızı B torbasında 2 yeşil , 5 kırmızı bilye vardır. Önce A torbasından bir bilye çekilip B torbasına atılıyor.sonra B torbasından bir bilye çekiliyor.
Buna göre B torbasından eşil bilye çekilmiş olma olasılığı kaçtır?
(cevap : 17/56)
S4) Bir torbada 4 sarı , 3 kırmızı ,2 bilye vardır. Torbadan aynı anda çekilen 3 bilyenin en az ikisinin aynı renkde olma olasılığı kaçtır?
(cevap : 5 / 7)
S5) ABCD bir dikdörtgen AB = 12 , BC = 5
ABCD dikdörtgeninde seçilen herhangi bir noktanın taralı bölgeye ait olmama olasılığı kaçtır?
(cevap : 1/2)
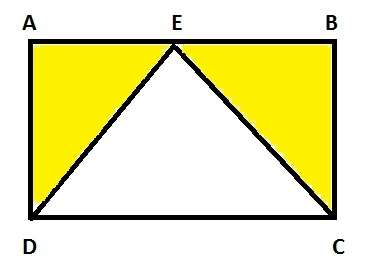
svsmumcu26 20:15 21 Ağu 2012 #2
9.Sınıfa gittiğimden (Olasılıktan pek bir şeyler bilmiyorum şuanlık ama) AED + EBC = EDC üçgeninin alanını vereceğinden sarı yerleri tek üçgen gibi düşünürüz diğer boş üçgeni de tek üçgen gibi (Alanları eşit 2 üçgen gibi yani) bu durumda sarıya gelmeme olasılığı 1/2 olur.Beyaza gelme olasılığıda (2 üçgen gibi kabul ettik) 1/2 olacaktır.
karinca_52 20:43 21 Ağu 2012 #3 9.Sınıfa gittiğimden (Olasılıktan pek bir şeyler bilmiyorum şuanlık ama) AED + EBC = EDC üçgeninin alanını vereceğinden sarı yerleri tek üçgen gibi düşünürüz diğer boş üçgeni de tek üçgen gibi (Alanları eşit 2 üçgen gibi yani) bu durumda sarıya gelmeme olasılığı 1/2 olur.Beyaza gelme olasılığıda (2 üçgen gibi kabul ettik) 1/2 olacaktır.
svsmumcu26 20:53 21 Ağu 2012 #4
Önemli değil ,ama aynı çözümlerin geleceğini düşünüyorum.(Mantıklı oldu bence ) 
karinca_52 21:02 21 Ağu 2012 #5 Önemli değil ,ama aynı çözümlerin geleceğini düşünüyorum.(Mantıklı oldu bence )
karinca_52 00:50 22 Ağu 2012 #6
2. ve 3. soruyu çözdüm.... diğer sorular için yardım bekliyorum arkadaşlar
gereksizyorumcu 01:20 22 Ağu 2012 #7
1.
P(A|B)=P(A∩B)/P(B) olduğunu biliyoruz. (sorunun formülü bu ama kafanızda kalmıyorsa bu formül çok direkt bir sonuç o yüzden soruları sağduyunuzla da aynı cevaba ulaşacak şekilde çözebilirsiniz, fomülü fazla kafanıza takmanıza gerek yok)
P(diğerinin mavi olma olasılığı|birinin sarı gelmesi)=P(diğerinin mavi olma olasılığı ∩ birinin sarı gelmesi)/P(birinin sarı gelmesi)
=P(birinin sarı birinin mavi gelmesi)/P(birinin sarı gelmesi)
=(2.4.5/(9.8))/(1-5.4/(9.8))=40/52=10/13
cevap farklı çıktı bişeyleri yanlış yazmadıysak cevap yanlış verilmiş olmalı , bi hata görüyorsanız belirtirseniz düzeltebiliriz. gerçi bu sorunun cevabının 1/2 olması çok mantıksız. düşünsenizse mavi gelme olasılığı ortada hiçbir bilgi yokken bile 1/2 den daha yüksek , siz bunun üzerine mavi ihtimalini daha da arttıracak bir altkümeye doğru geçiş yapıyorsunuz. neyse.
4.
sorulan olasılık 1-P(hepsinin farklı renkte olması) şeklinde de hesaplanabilir
P(hepsinin farklı renkte olması)=(4.3.2).3!/(9.8.7)=2/7 bulunur
öyleyse sorulan olasılık 1-2/7=5/7 olur
5.
bu soru yukarıda çözülmüş aynısını yazacağım ama sırf içiniz rahat etsin diye yazıyorum.
taralı alan denilen sarı yerlerse bu herhangi bir dikdörtgende toplam alanın yarısıdır.
bir bölgenin içinde (rastgele) seçilen bir noktanın bu bölgenin herhangi bir altbölgesine düşme ihtimali, o altbölgenin alanının tüm alana oranı olarak hesaplandığına göre
sorulan olasılık 1/2 bulunur.
P(A|B)=P(A∩B)/P(B) olduğunu biliyoruz. (sorunun formülü bu ama kafanızda kalmıyorsa bu formül çok direkt bir sonuç o yüzden soruları sağduyunuzla da aynı cevaba ulaşacak şekilde çözebilirsiniz, fomülü fazla kafanıza takmanıza gerek yok)
P(diğerinin mavi olma olasılığı|birinin sarı gelmesi)=P(diğerinin mavi olma olasılığı ∩ birinin sarı gelmesi)/P(birinin sarı gelmesi)
=P(birinin sarı birinin mavi gelmesi)/P(birinin sarı gelmesi)
=(2.4.5/(9.8))/(1-5.4/(9.8))=40/52=10/13
cevap farklı çıktı bişeyleri yanlış yazmadıysak cevap yanlış verilmiş olmalı , bi hata görüyorsanız belirtirseniz düzeltebiliriz. gerçi bu sorunun cevabının 1/2 olması çok mantıksız. düşünsenizse mavi gelme olasılığı ortada hiçbir bilgi yokken bile 1/2 den daha yüksek , siz bunun üzerine mavi ihtimalini daha da arttıracak bir altkümeye doğru geçiş yapıyorsunuz. neyse.
4.
sorulan olasılık 1-P(hepsinin farklı renkte olması) şeklinde de hesaplanabilir
P(hepsinin farklı renkte olması)=(4.3.2).3!/(9.8.7)=2/7 bulunur
öyleyse sorulan olasılık 1-2/7=5/7 olur
5.
bu soru yukarıda çözülmüş aynısını yazacağım ama sırf içiniz rahat etsin diye yazıyorum.
taralı alan denilen sarı yerlerse bu herhangi bir dikdörtgende toplam alanın yarısıdır.
bir bölgenin içinde (rastgele) seçilen bir noktanın bu bölgenin herhangi bir altbölgesine düşme ihtimali, o altbölgenin alanının tüm alana oranı olarak hesaplandığına göre
sorulan olasılık 1/2 bulunur.
karinca_52 01:51 22 Ağu 2012 #8
tşkrler
svsmumcu26 11:20 22 Ağu 2012 #9
Tamam doğru çözmüşüm Saolun hocam
Saolun hocam