ikinci dereceden denklemler

1) 3^x+x²-4=0 denkleminin kaç tane reel kökü vardır?

2) x⁴-5x²+m=0 denkleminin birbirinden farklı dört reel kökü vardır. buna göre m sayısı kaç farklı tam sayı değer alabilir?

3) x²-mx+360=0 denkleminin kökleri birer tam sayıdır. Buna göre m sayısı kaç farklı değer alabilir?

4) k≠3 olmak üzere, y=(k-3)x²-4x+1-k parabolleri A ve B gibi sabit iki noktadan geçtiğine göre AB doğrusunun denklemi nedir?

bakan yok mu daha ya

Kendi soruna mesaj yazdığın için cevaplanmış olarak gözüküyor. Bu yüzden cevaplanmamış sorularda gözükmüyor.
C.1
Deneyerek yaptım da başka türlü bir yoldan yapılır mı, aklıma hiç bir şey gelmedi.
x=1 için denklem sağlanır.
x değerleri büyüdükçe 3^x ifadesi de büyüyecektir x^2 ifadesi ise negatif olamayacağından başka durumlarda 4 bulunamaz.
Bu yüzden sadece 1 reel kökü vardır diye düşünüyorum.
C.2
x⁴-5x²+m=0
Yukarıdaki ifadenin 4 ayrı reel kökü var ise;
Delta>0
x²=t olmak üzere;
t²-5t+m=0
Delta>0 ise;
25-4m>0
25/4>m

4 ayrı reel kökün toplamı=0
Demek ki kökler;
x₁,-x₁,x₂,-x₂ durumunda.
Çarpımı=sabit terim/başkat sayısı=m=(x₁.x₂)²
Buna göre;
m>0 olmalı.(Çünkü kareli bir ifade negatif olamaz.Ayrıca m=0 da olamaz. O zaman farklı kökler bulunmaz.Yani bütün kökler 0,0,0,0 olur.)
Buna göre;
25/4>m>0
m;1,2,3,4,5,6 olabilir.
Yani 6 farklı değer vardır.
Emin olmamakla birlikte çözümüm böyle.***

Not:Kökler çarpımı daima Sabit terim/Baş kat sayısıdır.
Denklemin derecesi çift ise; kökler çarpımı=Sabit terim/Baş kat sayısı
Denklemin derecesi tek ise; kökler çarpımı=(-)Sabit terim/Baş kat sayısı

C.3
x²li bir ifade olduğundan 2 kökü vardır. Kökler tam sayı olduğunda göre;
Delta≥0 dır.
m²-4.360>0
12√10≥m≥-12√10
m de tam sayı olmalı.
Bu durumda m=-12,-11,.....0,1,....12=>25 tane değer alabilir.
Emin olmamakla birlikte çözümüm böyle**
**Bu sorular hangi kaynaktan bana özel mesaj atarsan sevinirim.

4. soru için aklıma hiçbir şey gelmedi. Çözümünü merakla bekliyorum.

teşekkürler ama sadece 2. sorunun cevabı doğru onu da anlamadım 3. soruda çarpanlarına ayırmak gerekiyor 360 ı ama ordan da cevap 48 olması lazım ama cevap 24 diyor.

Başka yardımcı olabilecek arkadaşlar var mı????

1)

.........

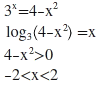
3)

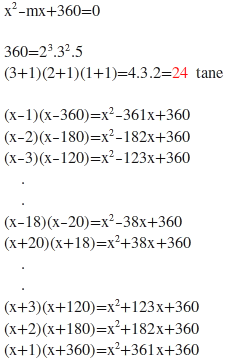
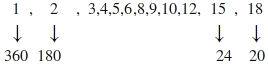
3)
x²-mx+360=0 kökleri tam sayı ise;
x1.x2=360
360=2³.3².5
4.3.2=24
24.2=48
Fakat bunun yarısını alırız. Çünkü toplam değerlerinde 2li durumları göz önüne almak gerekir;
360,1
180,2
90,4
45,8 ...... vb gibi. 48 tam sayı bölenlerinin 2li toplamlarının yarısı aynı sonucu verir.

4)

tamam hepsini anladım sağolun