S-1) a ve b aralarında asal doğal sayıdır. (2a+1).(b-2)=30 ise a+b toplamı kaç farklı değer alır? 2
S-2) M bir doğal sayı olmak üzere, (5-m)!+(m-2)! Toplamının alabileceği kaç farklı değer vardır? 2
S-3) 50!=(3a).(5b).c ifadesinde a,b,c birer doğal sayıdır. Buna göre a+b toplamının alabileceği en büyük değer kaçtır? 34
S-4) 25!+26!/(3x)=y ifadesinde x doğal sayıdır. Buna göre x in kaç farklı değeri için y pozitif tam sayı olur? 14
teşekkürler arkadaşlar
S-2) M bir doğal sayı olmak üzere, (5-m)!+(m-2)! Toplamının alabileceği kaç farklı değer vardır? 2
S-3) 50!=(3a).(5b).c ifadesinde a,b,c birer doğal sayıdır. Buna göre a+b toplamının alabileceği en büyük değer kaçtır? 34
S-4) 25!+26!/(3x)=y ifadesinde x doğal sayıdır. Buna göre x in kaç farklı değeri için y pozitif tam sayı olur? 14
teşekkürler arkadaşlar
C-1)
1.30
2.15
3.10
5.6
Tam tersleri de olabilir.
2a+1=1 olursa a=0 olur. şartımızı sağlamaz.
2a+1=2 olursa a=1/2 olur. Şartı sağlamaz.
2a+1=3 olursa a=1 olur ve b-2=10 olduğunda aralarında asal şartını sağlar.
2a+1=5 olursa a=2 olur. Bu şartımızı sağlar. b-2=6 olduğunda ise b=8 olur aralarında asal şartımızı sağlamaz.
Şimdide diğerlerine bakalım.
2a+1=30 olursa a tam sayı çıkmaz dolayısıyla asal diyemeyiz.
2a+1=15 olursa a=7 olur şartımızı sağlar b-2=2 olursa b=4 olur. 4 ve 7 aralarında asaldır.
2a+1=10 olursa a tam sayı olmaz.
2a+1=6 a tam sayı olmaz.
Dolayısıyla 2 tane a+b toplamı vardır.
C-2)
(5-m)!+(m-2)!
m=1 olamaz çünkü faktoriyel negatif olamaz.
m=2 olabilir. İkisi de pozitif olur. Yani m=5'e kadar değerle olabilir.
m=2,3,4,5 olabilir.
Bize toplamın kaç farklı değer alacağını sormuş m=2 ve m=5 için aynı sonuçları verir. ve m=3 ve m=4 içinde aynı değerleri vereceğinden 2 farklı toplam olduğunu söyleyebiliriz.
C-3)
a için 50! içerisindeki 3 sayılarını bulmamız gerekr bunun için 3'e bölüp kalanlara bakarız.
16+5+1=22 olur.
b için ise 50! içinde 5 sayılarına bakarsak
10+2=12 olur
12+22=34 bulunur.
C-4)
25!+26!/(3x)=y
[25!(1+26)]/3x
25!.27/3x
25! içerisinde 10 tane 3 çarpanı vardır. 27 den ise 3 tane gelebilir. x=0 da olabileceğinden
x 14 farklı değer alır.
1.30
2.15
3.10
5.6
Tam tersleri de olabilir.
2a+1=1 olursa a=0 olur. şartımızı sağlamaz.
2a+1=2 olursa a=1/2 olur. Şartı sağlamaz.
2a+1=3 olursa a=1 olur ve b-2=10 olduğunda aralarında asal şartını sağlar.
2a+1=5 olursa a=2 olur. Bu şartımızı sağlar. b-2=6 olduğunda ise b=8 olur aralarında asal şartımızı sağlamaz.
Şimdide diğerlerine bakalım.
2a+1=30 olursa a tam sayı çıkmaz dolayısıyla asal diyemeyiz.
2a+1=15 olursa a=7 olur şartımızı sağlar b-2=2 olursa b=4 olur. 4 ve 7 aralarında asaldır.
2a+1=10 olursa a tam sayı olmaz.
2a+1=6 a tam sayı olmaz.
Dolayısıyla 2 tane a+b toplamı vardır.
C-2)
(5-m)!+(m-2)!
m=1 olamaz çünkü faktoriyel negatif olamaz.
m=2 olabilir. İkisi de pozitif olur. Yani m=5'e kadar değerle olabilir.
m=2,3,4,5 olabilir.
Bize toplamın kaç farklı değer alacağını sormuş m=2 ve m=5 için aynı sonuçları verir. ve m=3 ve m=4 içinde aynı değerleri vereceğinden 2 farklı toplam olduğunu söyleyebiliriz.
C-3)
a için 50! içerisindeki 3 sayılarını bulmamız gerekr bunun için 3'e bölüp kalanlara bakarız.
16+5+1=22 olur.
b için ise 50! içinde 5 sayılarına bakarsak
10+2=12 olur
12+22=34 bulunur.
C-4)
25!+26!/(3x)=y
[25!(1+26)]/3x
25!.27/3x
25! içerisinde 10 tane 3 çarpanı vardır. 27 den ise 3 tane gelebilir. x=0 da olabileceğinden
x 14 farklı değer alır.
3)
50!=(3a).(5b).c
50! içindeki 3 çarpanları: 50/3=16, 16/3=5, 5/3=1, 16+5+1= 22
50! içindeki 5 çarpanları: 50/5=10, 10/5=2, 10+2= 12
a+b=22+12= 34
50!=(3a).(5b).c
50! içindeki 3 çarpanları: 50/3=16, 16/3=5, 5/3=1, 16+5+1= 22
50! içindeki 5 çarpanları: 50/5=10, 10/5=2, 10+2= 12
a+b=22+12= 34
5)

27=3³
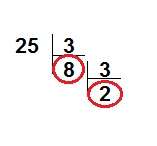
25!.27 çarpımı içinde:
(8+2)+3=13 tane 3 çarpanı var.
x : 0 , 1 , 2 , . . . , 12 , 13
14 tane.
25!+26!
3x
=y
25!(1+26)
3x
=y
27=3³
25!.27 çarpımı içinde:
(8+2)+3=13 tane 3 çarpanı var.
x : 0 , 1 , 2 , . . . , 12 , 13
14 tane.
teşekkürler arkadaşlar çok sağolun
Diğer çözümlü sorular alttadır.
