Kardelen91 00:59 29 Eki 2012 #1
bu esitlikleri ispat etmem gerekiyor
konuyu dogru yere acip acmadigimdan emin degilim ama yardimci olacak arkadaslara simdiden tesekkurler
Sinem.
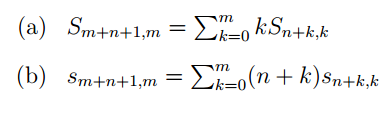
konuyu dogru yere acip acmadigimdan emin degilim ama yardimci olacak arkadaslara simdiden tesekkurler
Sinem.
gereksizyorumcu 02:56 29 Eki 2012 #2
burada Stirling Sayılarının tanımından kaynaklanan rekürans denkliği yazarsanız istediğiniz sonuca direkt ulaşıyorsunuz.
Sn+1,k=k.Sn,k+Sn,k-1
sn+1,k=n.sn,k+sn,k-1 olduğunu biliyoruz (*)
bu eşitliklerde n+1 yerine m+n+1 ve k yerine de m yazılırsa istenen sonuca ulaşılır ya da ilki için kısaca yazayım
m=1 için doğru
m=k için Sk+n+1,k=∑ olsun
m=k+1 için
Sk+1+n+1,k+1
=(k+1).Sk+n+1,k+1+Sk+n+1,k
=(k+1).Sk+n+1,k+1+∑
bu da verilen ifadeye eşit olur indisi bir tane fazla ilerletmek yetecektir.
(*) bu eşitlikler nereden geliyor diye düşünüyorsanız Stirling Sayılarının neyi ifade etttiğine bakmanız gerekir. bunları kabul olarak almayacaksanız kısaca açıklayabiliriz ama gerek olacağını sanmıyorum.
Sn+1,k=k.Sn,k+Sn,k-1
sn+1,k=n.sn,k+sn,k-1 olduğunu biliyoruz (*)
bu eşitliklerde n+1 yerine m+n+1 ve k yerine de m yazılırsa istenen sonuca ulaşılır ya da ilki için kısaca yazayım
m=1 için doğru
m=k için Sk+n+1,k=∑ olsun
m=k+1 için
Sk+1+n+1,k+1
=(k+1).Sk+n+1,k+1+Sk+n+1,k
=(k+1).Sk+n+1,k+1+∑
bu da verilen ifadeye eşit olur indisi bir tane fazla ilerletmek yetecektir.
(*) bu eşitlikler nereden geliyor diye düşünüyorsanız Stirling Sayılarının neyi ifade etttiğine bakmanız gerekir. bunları kabul olarak almayacaksanız kısaca açıklayabiliriz ama gerek olacağını sanmıyorum.
Kardelen91 17:16 01 Kas 2012 #3
Cevabınız için çok teşekkürler. Bana soruyu çözmemde çok yardımcı oldunuz.