Soru 1
a,b,c,d,e,f birbirinden farklı rakamlar olmak üzere ab , cd ve ef iki basamaklı sayıların toplamı en çok kaç olabilir ?
Çözüm
ab , cd , ef sayılarımızın en büyük olması için ilk öncelikle onlar basamakları alabilecekleri değerin en büyüğünü almalılar ki büyük sayılar elde edelim.
a=9
c=8
e=7 diyelim.
9b , 8d , 7f şimdide kalan harflere rakamlar atayalım b=6 olsun.(Rakamları farklı diyor.)
96 , 85 , 74 olursa alabilecekleri en büyük değerleri almış olurlar.
Bu değerleri toplarsak 96+85+74 = 255 bulunur.(En büyük değer)
------------------------------MT------------------------------
Soru 2
Rakamları birbirinden farklı , rakamları çarpımı 108 olan üç basamaklı en büyük doğal sayı ile en küçük doğal sayının toplamı kaçtır ?
Çözüm
Bu sayımız abc olsun.Bundan önceki örnekte açıkladığım gibi sayının en büyük olması için sırasıyla yüzler-onlar-birler basamağının alabilecekleri en büyük değerleri almaları gerekir.
a.b.c = 108 ise a=9 b=6 c=2 olursa bu koşul sağlanacaktır.(En büyük) aynı sayıyı bir de tersine çevirirse 269 'u elde ederiz bu da alabileceği en küçük değer olur.
962+269=1231 bulunur.
------------------------------MT------------------------------
Soru 3
Dört basamaklı bir sayı ile beş basamaklı bir sayının çarpımı en çok kaç basamaklı bir sayıdır ?
Çözüm
1.Yol
En çok basamağa ulaşmak için sayıları en büyük seçmeliyiz.
9999.99999 bu koşulu sağlar çarpımları ise 9 basamaklı bir sayıdır.
2.Yol
Bunu ilk önce bir örnekle açıklayalım.
9 ile 2'nin çarpımını misal getirelim.
Çarpımları 18 olur değil mi ? Bu durumda 6 , bir basamaklı 2 bir basamaklı iken çarpımları en çok basamak sayılarının 1 fazlası kadar yani 2 basamaklı olur.
Bir de 9 ile 0'ın çarpımını misal getirelim.
Bu durumda da 9 ile 0 ' birer bir basamaklı sayıyken çarpımları en az 1 basamaklı olan 0'a eşit olur değil mi yani 1+1-1 = 1 basamaklı bulunur yine.
Şöyle bir kural verelim
m ve n 2 basamaklı sayılar olmak üzere çarpımları en fazla m+n iken en az m+n-1 olur.
O halde 2.yolumuzla da şöyle çözebiliriz(En çok olması için)
Birisi 4 basamaklı diğeri 5 basamaklı en fazla ise (m+n)=9 basamaklı diyebiliriz.
------------------------------MT------------------------------
Soru 4
a,b,c asal sayılardır.a<b<c şartını sağlayan kaç farklı abc üç basamaklı sayı vardır ?
Çözüm
Asal rakamlarımız {2,3,5,7}
İstersek sıra sıra değerler veririz.235 ,237,257,357 olmak üzere 4 tane buluruz.
İstersekte kombinasyon kullanarak yapabiliriz.
Bunun için ilk önce 4 sayımızdan 3'ünü seçeriz.C(4,3)=4 farklı biçimde seçilir atıyorum 235 rakamlarıyla bu şekilde yalnızca 1 tane yazabiliyoruz e bunun gibi 4 tane seçebiliyormuşuz 4.1=4 tane bulunur...
------------------------------MT------------------------------
Soru 5
Üç basamaklı abc sayısı rakamları toplamına bölündüğünde bölüm 17 ve kalan 5 bulunuyor.Buna göre a+b+c toplamı kaçtır ?
Çözüm
Şöyle düşüneceğiz , bölünen = bölüm.bölen + kalan
abc=(a+b+c).17+5
100a+10b+c=17a+17b+17c+5
83a=7b+16c+5 eşitliğinin sağlanması için
a=1 , b=2 ve c=4 olmalıdır.
a+b+c=1+2+4=7 olmalıdır.
------------------------------MT------------------------------
Soru 6
ab ve cd iki basamaklı sayılardır , ab.cd çarpımında b , 2 arttırılıp , a 3 azaltılırsa çarpımın sonucu 364 azalıyor.Buna göre 2a+3d toplamı kaçtır ?
Çözüm
B birler basamağı olduğundan 2 arttırılması sayı 2 arttırır.
A onlar basamağı olduğundan 3 azaltılması 3.10 sayıyı 30 azaltır.
(AB+2-30).CD=AB.CD-364
(AB-28).CD=AB.CD-364
ABCD-28CD=ABCD-364
-28CD=-364
CD=13
C=1
D=3 bulunur.
2c+3d=2+9=11 bulunur.
------------------------------MT------------------------------
Soru 7
Altı basamaklı bir sayı üç basamaklı bir sayıya bölündüğünde kalan sayı en fazla kaç basamaklıdır ?
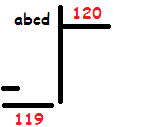
Çözüm
Görüldüğü gibi kalan bölenden küçük olduğundan en fazla 3 basamaklı olabilir.
------------------------------MT------------------------------
Soru 8
3,4,5,6 ve 7 rakamları kullanılarak yazılabilen rakamları farklı tüm iki basamaklı tek doğal sayıların toplamı kaçtır ?
Çözüm
Birler basamağı 3 olanlar 43 53 63 73 olmak üzere 4 tanedir.Aynı şekilde
Birler basamağı 5 olanlar 4 tanedir.
Birler basamağı 7 olanlar 4 tanedir. Toplamda 12 tane sayı vardır.
Birler basamağı 3 olanlara bakalım
Bu sayıların toplamı 12+40+50+60+70 = 232 bulunur.
Birler basamağı 5 olanlara bakalım.
45 35 65 75 olmak üzere = 20+40+30+60+70 = 220 bulunur.
Birler basamağı 7 olanlara bakalım
47 37 67 57 olmak üzere 28+40+30+60+50 = 208
232+220+208 = 260 bulunur.