bibliophile 23:06 08 Tem 2013 #1
1) (2,3)5 sayısının 10 tabanında eşiti ? (11/4)
2) 22! sayısının 23 ile bölümünden kalan kaçtır ? (22)
3)6 sayı tabanı olmak üzere (ab1c)6 sayısı 5 ile tam bölünebildiğine göre a+b+c toplamı en çok kaçtır ? (14)
4) 21!+10.19!-14 sayısının 43 ile bölümünden kalan kaçtır ? (29)
5) 103!-3 sayısı 5 tabanında yazıldığında elde edilecek sayıların son dört basamağındaki rakamlar on tabanında kaçtır ? (14)
2) 22! sayısının 23 ile bölümünden kalan kaçtır ? (22)
3)6 sayı tabanı olmak üzere (ab1c)6 sayısı 5 ile tam bölünebildiğine göre a+b+c toplamı en çok kaçtır ? (14)
4) 21!+10.19!-14 sayısının 43 ile bölümünden kalan kaçtır ? (29)
5) 103!-3 sayısı 5 tabanında yazıldığında elde edilecek sayıların son dört basamağındaki rakamlar on tabanında kaçtır ? (14)
sentetikgeo 23:38 08 Tem 2013 #2
1)
sentetikgeo 23:40 08 Tem 2013 #3
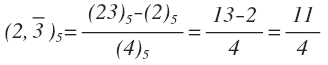
2)
p asal ise (p-1)!≡p-1(mod p)
Yani 22!≡22(mod23)
p asal ise (p-1)!≡p-1(mod p)
Yani 22!≡22(mod23)
sentetikgeo 23:44 08 Tem 2013 #4
3)
n tabanındaki sayı (n-1)'e bölünüyorsa rakamları toplamı (n-1)'e bölünür.
Çünkü sayıyı çözümlersek
a.6³+b.6²+6+c
6'nın her kuvveti mod5'de 1'e denktir. Öyleyse bu sayı mod5'te a+b+1+c'ye denktir.
a+b+1+c sayısı 5'e bölünüyorsa ve a<6,b<6,c<6 ise a+b+c en çok 14 olur.
n tabanındaki sayı (n-1)'e bölünüyorsa rakamları toplamı (n-1)'e bölünür.
Çünkü sayıyı çözümlersek
a.6³+b.6²+6+c
6'nın her kuvveti mod5'de 1'e denktir. Öyleyse bu sayı mod5'te a+b+1+c'ye denktir.
a+b+1+c sayısı 5'e bölünüyorsa ve a<6,b<6,c<6 ise a+b+c en çok 14 olur.
sentetikgeo 23:46 08 Tem 2013 #5
4)
21!+10.19!=420.19!+10.19!=430.19! yani 43'e bölünür.
Öyleyse bu sayının 14 eksiği 43'e bölününce 29 kalanını verir.
21!+10.19!=420.19!+10.19!=430.19! yani 43'e bölünür.
Öyleyse bu sayının 14 eksiği 43'e bölününce 29 kalanını verir.