Açı-Kenar Bağıntıları(Üçgen)

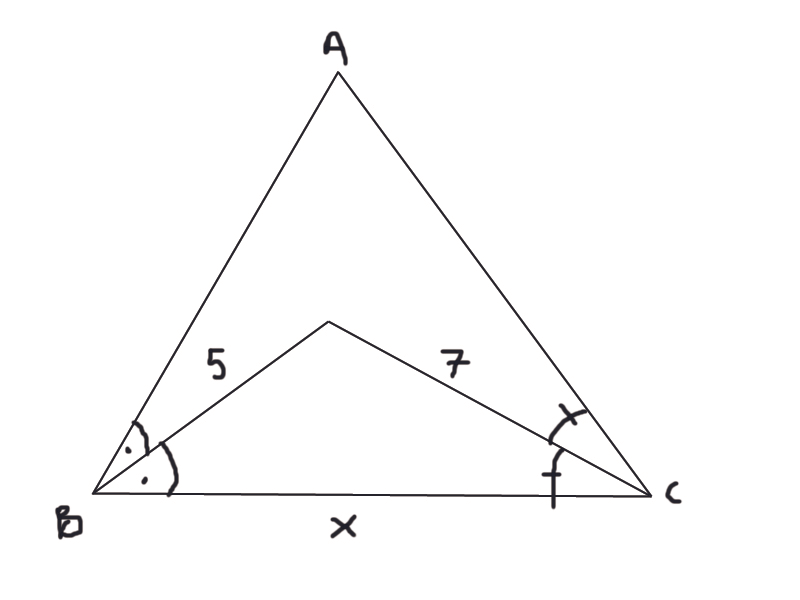
ABC bir üçgen [BD] ve [CD] açıortay
lBDl=5cm
lCDl=7cm

Verilere göre, x'in alabileceği tam sayı değerleri toplamı?

Cevap:30



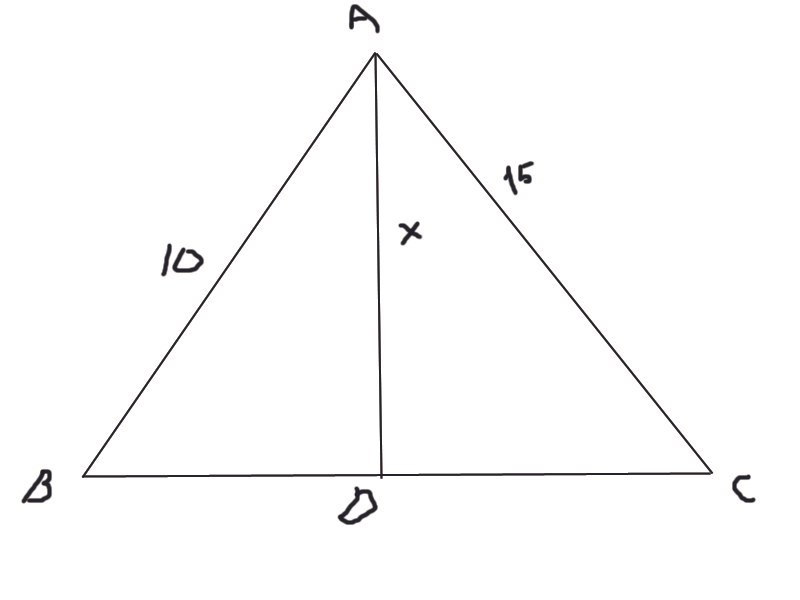
ABC bir üçgen 2lCDl=3lBDl

lABl=10cm

lACl=15cm

ise x'in alabileceği en büyük tamsayı değeri?

Cevap:11

2.
iki kenarı ve iç açıortayı verilen bir üçgende 0<na<2bc/b+c eşitliği geçerlidir.(Bunu şöyle ispatlayabiliriz,ufak bir işim var sonra yazarım buraya.)
0<n<300/25
0<n<12 şeklinde yazıliablir.
n maksimum 11 bulunur.

1.
içerideki üçgende tepe açısı geniş açı olduğundan x^2>74 olmalıdır. kısacası x>√74 (x>8.32 civarı) olmalıdır.Diğer yandan üçgen eşitsizliği gereği 2<x<12 olması gerektiği de bilinmektedir.
9,10,11 değerlerini alabilir toplamda 30 yani.

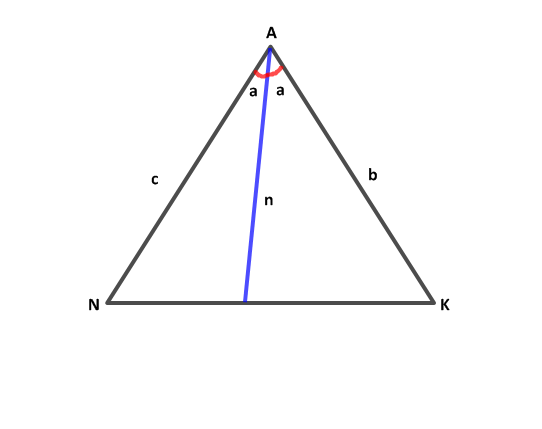
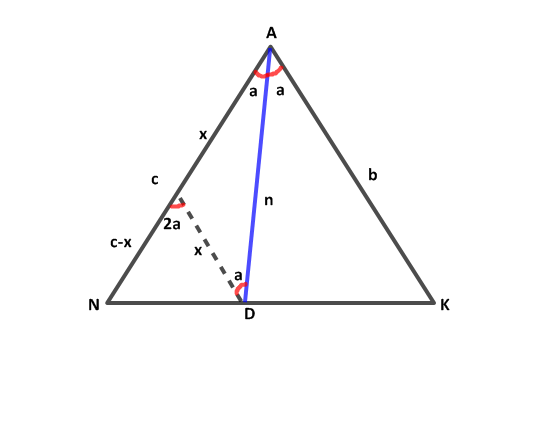
Kanıt.
D'den NA'ya çekilen uzantı NA'yı L'de kessin.
Verilen iki üçgenin (biri ufak biri büyük benzerliğinden c-x/c = x/b olr.Düzenlenirse bc-bx=cx olur ki buradan x=bc/b+c çıkar.(ALD) üçgeninde üçgen eşitsizliği gereği 0<n<2x olduğundan 0<na<2bc/b+c şeklindedir.

Teşekkür ederim. Ama soruda bir açıortaylık belirtilmemiş, neye göre karar veriyoruz?

AB/BD=AC/DC olduğundan iç açıortay belirtir.

Hımm anladım. Tekrardan teşekkürler.

rica ederim.

Bir soru daha sorayım. Normal bir ABC üçgenimiz var. Bu üçgenin bir kenarı 8, diğer kenarı 5cm. Üçüncü kenarı x cm. Bu x'i gören açı, 60 dereceden büyük deniyor. O zaman x'in alabilecği tam sayı değerleri toplamı kaçtır?

Cevap:50

5-7-8 üçgeni özel bir üçgendir kosinüs teoreminden ispatlayabilirsiniz 7nin karşısı 60* görür.
üçüncü kenar 60* olsaydı 7 olurdu büyük olduğuna göre >7 olmalıdır üçgen eşitsizliğinden 13>x>7 dersek 12+11+10+9+8 => 50 bulunur.