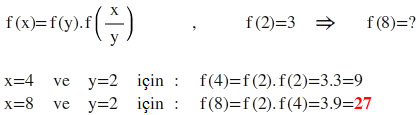fonksiyonlar

1-) f : R - R ve g : R - R olmak üzere ,
f(x) = 7x -12
g(x+2) = f(x+3) olduğuna göre ,
(fog)(4) değeri kaçtır?
a)149
b)140
c)128
d)101
e)79
2-) f:R /(a) - R /(b)
f(x)= 5 - 2x / 3x- 4 birebir ve örten fonksiyondur.
Buna göre , a-b farkı kaçtır?
a)-4
b)-6/5
c)8/3
d)2
e)4
3-)f(x) = f(y) . f(x / y) olarak verilen f fonksiyonu için f(2) = 3 olduğuna göre , f(8) kaçtır?
a)64
b)54
c)27
d)16
e)12

4-)f(x) = x. f(x+1) ve f(1) = 10! olduğuna göre , f(10) kaçtır?
a)5
b)10
c)15
d)20
e)25


Ayrıntılı açıklarsanız sevinirim

1-) f : R - R ve g : R - R olmak üzere ,
f(x) = 7x -12
g(x+2) = f(x+3) olduğuna göre ,
(fog)(4) değeri kaçtır?

g(4) için x'e 2 verelim: g(4)=f(5) olur. f(5)=7.5-12 = 35-12 = 23
f(23)=7.23-12=161-12=149 çıkar. (A)

2-) f:R /(a) - R /(b)
f(x)= 5 - 2x / 3x- 4 birebir ve örten fonksiyondur.
Buna göre , a-b farkı kaçtır?

birebir ve örten ise her elemen farklı eleman ile bağlanacak ve değer kümemizde boşta eleman kalmayacaktır. Buna göre
1.durumda a'yı bulmak için 5-2x/3x-4 fonk. tanımsız yapan değer bulunmalıdır. Tanımsız yapan değer ile birlikte fonk. sonucu yoktur.
Bunn için paydanın kökünü bul sıfıra eşitleyerek ( payda 0 a eşit olamaz. ) a=4/3
2.durumda b'yi bulmak için fonk. tersinin tanımsız yapan değerini bulmak gerekir. Fonk tersi : 4x+5/3x+2'dir. burda b=-2/3'dür.
a-b =4/3 +2/3 = 2 çıkar. (D)

4-)f(x) = x. f(x+1) ve f(1) = 10! olduğuna göre , f(10) kaçtır?

f(1)=f(2)
f(2)=f(3).2
.. ...
f(9)=f(10).9
x___________
f(1).f(2)....f(9)=f(2).f(3)....f(10).2.3.4.5....9
10!=f(10).9!
f(10)=10 çıkar. ( B)

teşekkürler 3. soruya da bakabilirsen sewinirim...

3)

teşekkür ederim hocam