Soru 1- x ve y pozitif tam sayılar.
20. y-1 = x²+2x olduğuna göre x+y toplamı en az kaç olur?
Şıklar : 14 16 18 21 24
(Sürekli 13 bulup duruyorum. x 8 y 5)
Soru 2- x+2 < y < 2x-8 ise ynin alabileceği en küçük tam sayı değeri kaçtır?
Şıklar : 6 8 13 14 15
Bunda da cevap 13'müş.
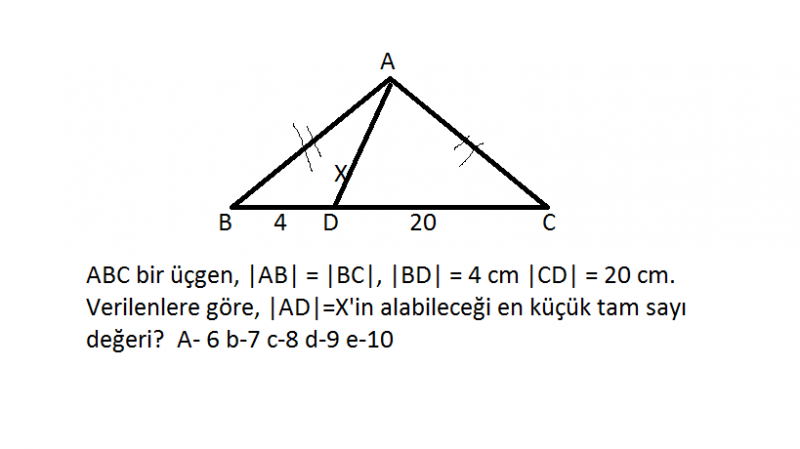
Soru 3-
Çok teşekkürler.