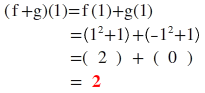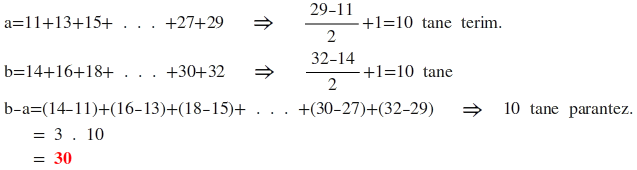fonksiyon

arslan 15:41 01 Ağu 2012 #1

f(x)=2x²-4x-m-1 (ifadenin hepsi karekök içinde)
fonksiyonunun en geniş tanım aralığı (-sonsuz,+sonsuz)
olduğuna gör e m nin alabileceği en büyük tam sayı değeri kaçtır?cvp-3
2-
f(x)=|x-2| ve g(x)=x-2 olmak üzere R-{2} de tanımlı
h(x)=(f/g)(x)
fonksiyonunun görüntü kümesi nedir?cvp{-1,1} ben bunu buldum ama neden parantez köşeli değil bunu açıklayabilir misiniz?

3-

f(x)={x²+1    x<2

      x       x≥2

g(x)={-x²+1     x≥0

       2       x<0

olduğuna göre (f+g)(1) değeri kaçtır?
cvp2
4-
A=11+13+15+...................+27+29
B=14+16+18+.......................+30+32
olduğuna göre hangisi doğrudur?
cvp b-a=30
5-
T=1.2+2.3+3.4+4.5+.................+19.20
olduğuna göre t toplamını oluşturan her bir teriminb 1.çarpanı 1 azaltılıp 2.çarpanı 1 arttırılırsa t değeri kaç azalır?38

svsmumcu26 15:56 01 Ağu 2012 #2

f(x)=|x-2| ve g(x)=x-2 olmak üzere R-{2} de tanımlı
h(x)=(f/g)(x)
fonksiyonunun görüntü kümesi nedir?

f(x)=|x-2| verilmiş o halde mutlak değer içindeki değeri bir pozitif bir de negatif çıkartmalıyız.

Pozitif için :: (x-2) olarak çıkar

Bu durumda h(x) = x-2 / x-2 = h(x)=1 çıkar

Negatif için :: -x+2 olarak çıkar.
Bu durumda ; h(x)= -(x-2) / (x-2) ) = -1 çıkar.

2Değer sağlıyor bunlar 1 ve -1 budurumda ; ÇK= {-1,1} olur.

kcancelik 16:40 01 Ağu 2012 #3

f(x)=√2x²-4x-m-1 tanım kümesi (-∞, ∞) ise bütün x gerçelleri için sağlanır. Çift dereceli kökün içi negatif olamaz. Düşünecek olursak, sadece tam kare ifadeler her gerçel sayı için pozitif veya sıfır olabilirler. Tam kare olarak çarpanlara ayırmalıyız:
Önce iki çarpanını ayıralım:
2x²-4x-m-1
2(x²-2x+(-m-1)/2)
(-m-1)/2=t dersek;
2(x²-2x+t) tam kare olmalı. x²-2x kısmının (x-1)² kısmından geldiğini görebilmemiz gerekir. O halde sabit kısım +1 olur. Buradan t=1 olursa;
-m-1=1.2
-m-1=2
-m=3
m=-3 olur.
Ayrıca ikinci sorudaki fonksiyon işaret fonksiyonu(sgn())dur. sgn(x)=|x|/x=x/|x| olarak tanımlanır. Dikkat ederseniz sadece -1 ve 1 değerleri çıkabilir. x=0 için tanımsızdır. Pratik durumlarda yardımcı olabilir.
İyi günler.