Fonksiyonlar

R den R ye,


f (x)= 4x-6, x≥2 ise ve ax+b, x<2 ise


fonksiyonu bire bir ve örtendir.

f⁻¹ (-7) = -1 ise, f⁻¹ (-19) kaçtır?

Soruda istenenlere göre x≥2, 4x-6 denklemini kullanamadım.Lütfen yardım edin.

f fonksiyonu bire bir ve örten olduğu zaman bu iki denklemi her ikisine de 2 değerini vererek birbirine eşitleyebiliyor muyuz? Bu soruyu uzun uğraşlar sonunda "özel tanımlı fonksiyonlar" konusunda verilen örnekler sayesinde çözebildim. Çözümüm şu şekilde:

fonksiyonun tersini bulmak için;

i-) x≥2
4x-6≥4.2-6
4x-6≥2

ii-) x<2
ax+b<2a+b

parçalı fonksiyonda bir taraf ≥2 olduğundan diğer taraftaki eşitsizlikte de < den sonra 2 gelmelidir. Yani;

2a+b=2 dir.

f (-1) = -7

-a+b =-7

a ve b değerlerini bulmak için;

2a+b=2
a-b=7

Buradan a=3 ve b=-4 bulunur.

Sonuç olarak,


f⁻¹ (x)=(x+6)\4, x≥2 ise ve (x-b)\a, x<2 ise

şeklinde yazdığımız f⁻¹ (x) fonksiyonunda a ve b değerlerini yerlerine koyduktan sonra x yerine -19 yazdığımızda,

f⁻¹ (-19)=[-19 - (-4)]\3 =-5

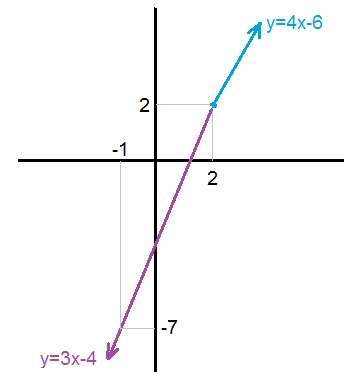
Mavi grafiğin ordinatları (y≥2),
örten fonksiyon olması için diğer grafikte y<2 olmalı.
Soru bunların yerine sürekli olmalı da diyebilirdi.
x, 2 'ye sağdan ve soldan yaklaşırken y 'ler 2 'ye yaklaşmalı.
Birebir olması ise her x 'in bir tane y değeri olmalı.