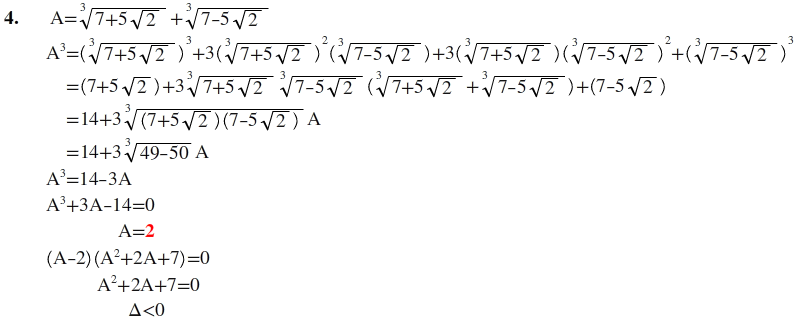1)a,b,c pozitif tamsayı ve beş basamaklı aabca sayısı 19 a tam bölündüğüne göre cb iki basamaklı sayısını kalansız bölen asal sayıların toplamı kactir?
2)A,B,C,D,E,F doğal sayılar olmak üzere
A.B=C+D+E ve E<F dir
Buna göre 6 basamaklı kaç ABCDEF sayısı yazılabilir?
3)x²-x+1=0 olduğuna göre x16+x²+3 ifadesinin değeri kaçtır? 2
4)∛7+5√2+∛7-5√2 işleminin sonucu kaçtır?2
5)a,b ve A birer doğal sayı olmak üzere,
34!=4a.3b.A ise a+b toplamı kaç farklı değer alabilir? 15,16,31,32,47
6)Her biri iki basamaklı olan 5 doğal sayının toplamı 265 olduğuna göre bu sayıların en küçüğü en çok kaçtır? 52
7)72! sayısı 3 tabanında kaç basamaklı bir sayıdır?54