1- A=|X+5|-|X-2| olduğuna göre A nın alabileceği kaç faklı tam sayı değeri vardır?
cevap 15
2- ||X|+3| + |-X|+|X|=24 denkleminin kökleri çarpımı kaçtır?
cevap -49
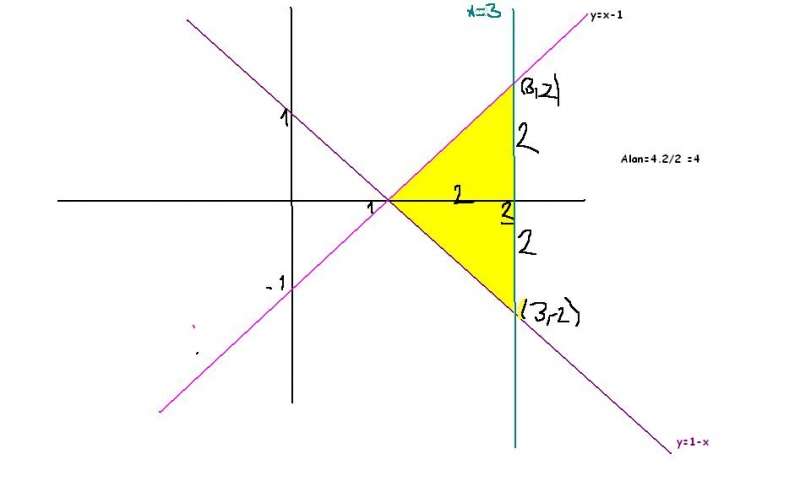
3- |y|=X-1 fonksiyonu ve x=3 doğruları ile sınırlanan kapalı alan kaç birim karedir?
cavap 4
4- |X2-X-6|≤|X+2| eşitsizliğini sağlayan kaç tane x tamsayısı vardır?
cevap 4
5-