sevde maydagil 20:49 02 Haz 2013 #1
1) Z: 5 + √2i karmaşık sayısının küpköklerine karşilık gelen noktaları köşe kabul eden geometrik şeklin alanı kaç birimkaredir ?
a) 15\4.√3 b) 7\2.√3 c)3√3 d)9\4.√3 e)2√3
2) 5 sakız 3 kardeşe dağıtılacaktır . her kardeşin en az 1 sakız alma olasılığı nedir?
a.6\7 b.5\7 c.4\7 d.3\7 e.2\7
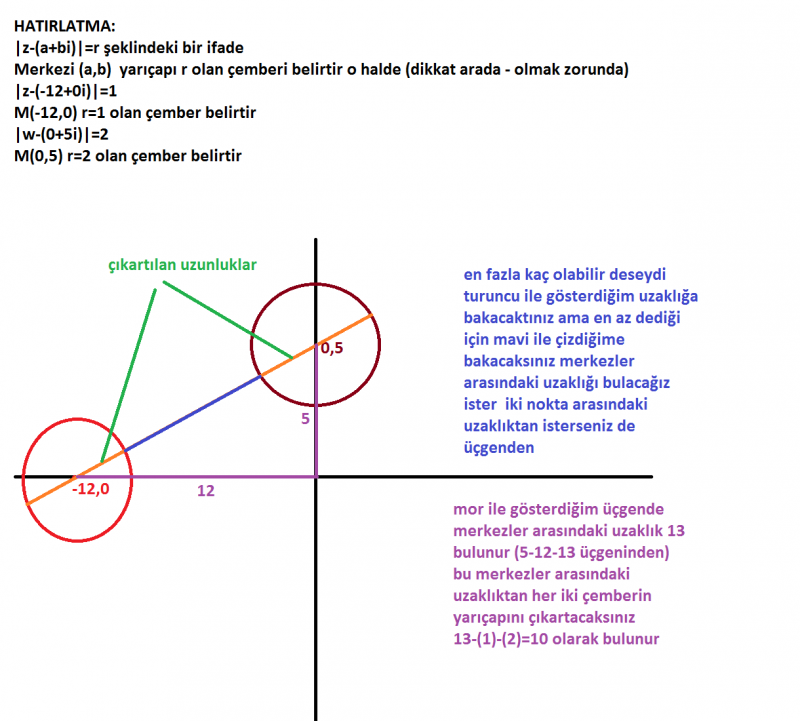
3) |z+12| = 1
|w-5i| = 2
eşitliğini sağlayan karmaşık sayılar için |z-w| en az kaçtır ?
a.16 b.13 c.10 d.7 e.5
4) yarıçapı 9 cm olan bir dairenin içine aynı merkezli ve herbiri bir öncekinin 1\3 ü kadar olan sonsuz daire çizilirse meydana gelen daire alanlarının toplamı kaç olur?
a.92pi b.729\8pi c.715\8pi d.88pi e.709\8pi
5) çevresi 60 cm olan daire dilimi şeklindeki bir kartonun alanının en büyük olması için dairenin yarıçapı kaç cm olmalıdır?
a.12 b.12,5 c.15 d.16 e.17,5
şimdiden ilginiz için çok teşekkür ederim
a) 15\4.√3 b) 7\2.√3 c)3√3 d)9\4.√3 e)2√3
2) 5 sakız 3 kardeşe dağıtılacaktır . her kardeşin en az 1 sakız alma olasılığı nedir?
a.6\7 b.5\7 c.4\7 d.3\7 e.2\7
3) |z+12| = 1
|w-5i| = 2
eşitliğini sağlayan karmaşık sayılar için |z-w| en az kaçtır ?
a.16 b.13 c.10 d.7 e.5
4) yarıçapı 9 cm olan bir dairenin içine aynı merkezli ve herbiri bir öncekinin 1\3 ü kadar olan sonsuz daire çizilirse meydana gelen daire alanlarının toplamı kaç olur?
a.92pi b.729\8pi c.715\8pi d.88pi e.709\8pi
5) çevresi 60 cm olan daire dilimi şeklindeki bir kartonun alanının en büyük olması için dairenin yarıçapı kaç cm olmalıdır?
a.12 b.12,5 c.15 d.16 e.17,5
şimdiden ilginiz için çok teşekkür ederim
2) TÜM DURUM:5 sakız 3 kardeşe kaç farklı şekilde şekilde dağıtılabilir
BİZDEN İSTENEN:5 sakız 3 kardeşe dağıtılacak.Her kardeşin en az bir tane alması önce tüm duruma bakalım oyucakları özdeş kabul ediyorum
ayraç yöntemi kullanacağız 5 sakız var 3-1=2 ayraç var (çocuk sayısının 1 eksiği)
5 sakız 2 ayraç x=sakız y=ayraç olsun
xxxxxyy bunları tekrarlı permütasyonla dizeceğiz 7!/5!.2!=21
tüm durum=21
bizden istenen her çocukta en az bir tane sakız olsun o halde her çocuğa 1 tane sakız verelim 5-3=2 sakız kalır bundan sonra yine ayraç kullanacağız
2 sakız 3-1=2 ayraç
xxyy tekrarlı permütasyondan 4!/2!.2!=6
bizden istenen=6
6/21=2/7 olarak bulunur
BİZDEN İSTENEN:5 sakız 3 kardeşe dağıtılacak.Her kardeşin en az bir tane alması önce tüm duruma bakalım oyucakları özdeş kabul ediyorum
ayraç yöntemi kullanacağız 5 sakız var 3-1=2 ayraç var (çocuk sayısının 1 eksiği)
5 sakız 2 ayraç x=sakız y=ayraç olsun
xxxxxyy bunları tekrarlı permütasyonla dizeceğiz 7!/5!.2!=21
tüm durum=21
bizden istenen her çocukta en az bir tane sakız olsun o halde her çocuğa 1 tane sakız verelim 5-3=2 sakız kalır bundan sonra yine ayraç kullanacağız
2 sakız 3-1=2 ayraç
xxyy tekrarlı permütasyondan 4!/2!.2!=6
bizden istenen=6
6/21=2/7 olarak bulunur
sevde maydagil 21:29 02 Haz 2013 #3
çok teşekkür ederiiim , çok da güzel açıklamışsın
sevde maydagil 22:02 02 Haz 2013 #7
tekrardan teşekkür ederim , çok yardımcı oldunuz
gereksizyorumcu 22:35 02 Haz 2013 #8 5) çevresi 60 cm olan daire dilimi şeklindeki bir kartonun alanının en büyük olması için dairenin yarıçapı kaç cm olmalıdır?
a.12 b.12,5 c.15 d.16 e.17,5
a.12 b.12,5 c.15 d.16 e.17,5
yarıçapa r , yayın açısına da a dersek
yay uzunluğu a.r , alanı ar²/2 olur
toplam çevre verilmiş ar+r+r=60 , buradan ar=60-2r yazılırsa
(60-2r).r/2 nin max olması isteniyor
max(30r-r²) , bu da türev alınırsa r=15 için max olduğu görülür.
bir diğer deyişle yay uzunluğu çevrenin yarısı olunca alan max olur. (ya da a=2 radyanken)
(bu yarıçap için alan ar.r/2=30.15/2=225 olur , 900/∏ den küçük)
sevde maydagil 22:24 03 Haz 2013 #9
Çok teşekkürleer.