türev4 soru çözümlü ama nerden geldiğini anlamadım

s-1)sin(cos3x)in = cos(cos3x).(-sin3x).3 'e nasıl dönüşür.


s-2)y=t²-t ve x=3t+1 verilmiş.d²y/dx² isteniyor.y'=2t-1/t sonradan 2/3 ü neden 3eböleriz.


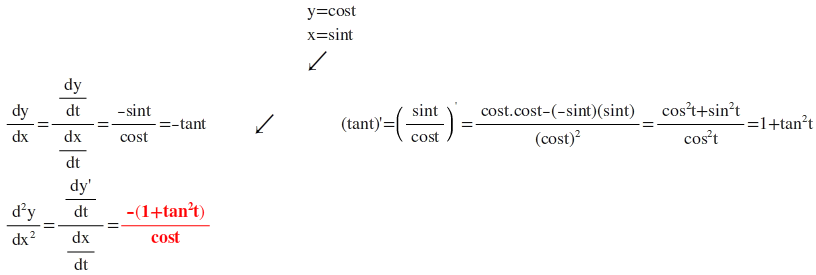
s-3)y=cost ve x=sint d²y/dx²=? -sint/cost=-tant bu nasıl ve nerden -(1+tan²)/cost ye dönüştü.


s-4)e^xy-3=0ın x=2 noktasındaki teğetinin denklemi?
-y.e^xy /x.e^xy =-x/y ise sonradan niye -1/2 yi 2ye bölüyoruz
nerden geldiklerini anlamadım .anlatırsanız sevinirim.

C-1

Buna zincir kuralı denir.
f ve g kapalı, sonlu bir I aralığı üzerinde diferansiyellenebilir olsun. d[f(g(x))]/dx=f'(g(x)).g'(x) olur.
[sin(cos(3x))]'
İlk olarak sinüsün türevini alalım:
cos(cos(3x))
Daha sonra sinüsün içinin türevini alıp onunla çarpmalıyız:
cos(cos(3x)).(-sin(3x))
Son olarak cos(3x)'in içinin türevini alıp çarpmalıyız:
cos(cos(3x)).(-sin(3x)).3
[f(g(h(x)))]'=f'(g(h(x))).g'(h(x)).h'(x) olması diyebiliriz.
İyi günler.

C-2

y=t²-t
x=3t+1
x-1=3t
(x-1)/3=t
y=((x-1)/3)²-(x-1)/3=(x²-2x+1)/9-(x-1)/3=(x²-2x+1-3x+3)/9=(x²-5x+4)/9
dy/dx=[(x²-5x+4)/9]'=1/9(2x-5)
d²y/dx²=d(dy/dx)/dx=[1/9(2x-5)]'=1/9(2)=2/9
İyi günler.

1)

2)

3)

4)

Elllllerinize sağlık Süleyman hocam.

Çözümlü Türev Soruları Türev Soruları ve Çözümleri
Tüm Etiketler