1)


2)


3)


Not: Cevaplarını bilmiyorum.

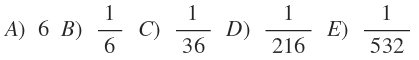
2)
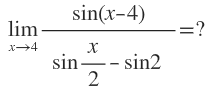
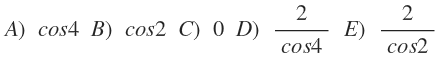
3)
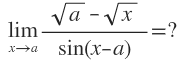
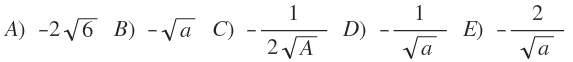
Not: Cevaplarını bilmiyorum.
C-3
(√a-√x)/sin(x-a)
Her iki tarafı payın eşleniği ile çarpalım:
(a-x)/[sin(x-a)(√a+√x)]
-(x-a)/[sin(x-a)(√a+√x)]
x->a'yı x-a->0 diye değiştirebiliriz, o halde lim(x->0)sinx/x=1'i kullanarak ifadenin limiti -1/(√a+√x)'tir. diyebiliriz.
x=a alırsak -1/2√a çıkar.
İyi günler.
C-2
x=4 koyarsak sin(4-4)/(sin4/2-sin2)=0/0 belirsizliği çıkar. L'Hôpital kullanalım:
[sin(x-4)]'=cos(x-4)
[sin(x/2)-sin(2)]'
sin2 sabit değer olacağından gider, diğer kısım için zincir kuralı kullanalım:
[sin(x/2)]'=cos(x/2).(x/2)'=cos(x/2)/2
cos(x-4)/[cos(x/2)/2]=2cos(x-4)/cos(x/2) oldu.
x=4 alırsak 2cos(0)/cos(2) olur. cos(0)=1 olduğundan sonuç 2/cos(2) olur.
İyi günler.
C-1
√6+√6+√x-3'ün eşleniği ile çarpalım:
6+√6+√x-9=-3+√6+√x olur. Payda ise (x-9)(√6+√6+√x+3) olur.
Bir kez daha eşleniği ile çarparsak pay -9+6+√x=-3+√x olur. Payda ise (x-9)(√6+√6+√x+3)(√6+√x+3) olur.
Tekrar eşlenik ile çarparsak pay x-9, payda (x-9)(√6+√6+√x)(√6+√x+3)(√x+3) olur.
x-9'lar sadeleşir. 1/(√6+√6+√x+3)(√6+√x+3)(√x+3) kalır.
x=9 alırsak;1/(6.6.6)=1/216 olur.
İyi günler.
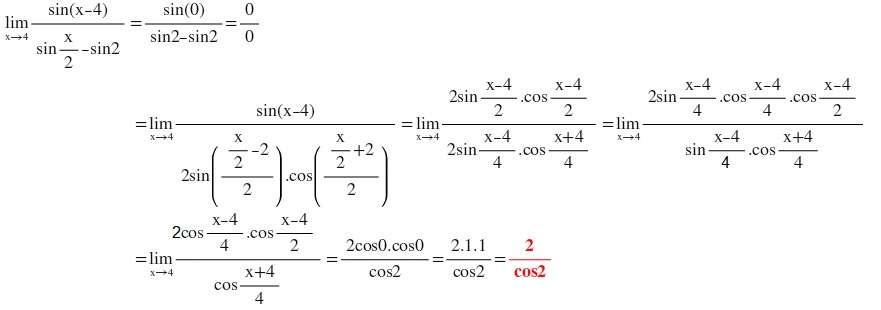
x=4 koyarsak sin(4-4)/(sin4/2-sin2)=0/0 belirsizliği çıkar. L'Hôpital kullanalım:
[sin(x-4)]'=cos(x-4)
[sin(x/2)-sin(2)]'
sin2 sabit değer olacağından gider, diğer kısım için zincir kuralı kullanalım:
[sin(x/2)]'=cos(x/2).(x/2)'=cos(x/2)/2
cos(x-4)/[cos(x/2)/2]=2cos(x-4)/cos(x/2) oldu.
x=4 alırsak 2cos(0)/cos(2) olur. cos(0)=1 olduğundan sonuç 2/cos(2) olur.
İyi günler.
[sin(x-4)]'=cos(x-4)
[sin(x/2)-sin(2)]'
sin2 sabit değer olacağından gider, diğer kısım için zincir kuralı kullanalım:
[sin(x/2)]'=cos(x/2).(x/2)'=cos(x/2)/2
cos(x-4)/[cos(x/2)/2]=2cos(x-4)/cos(x/2) oldu.
x=4 alırsak 2cos(0)/cos(2) olur. cos(0)=1 olduğundan sonuç 2/cos(2) olur.
İyi günler.
2)
Kcacelik, ilerde 12. sınıf senin için sıkıcı geçebilir.
Tebrikler.

Kcacelik, ilerde 12. sınıf senin için sıkıcı geçebilir.
Tebrikler.
2)
Kcacelik, ilerde 12. sınıf senin için sıkıcı geçebilir.
Tebrikler.

Kcacelik, ilerde 12. sınıf senin için sıkıcı geçebilir.
Tebrikler.

