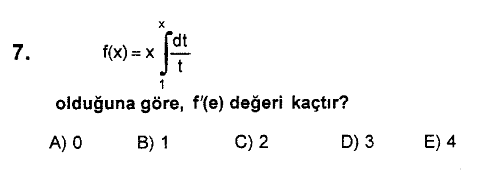
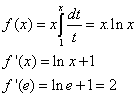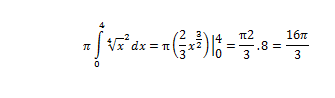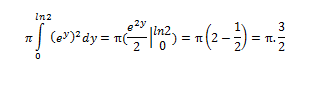Değerli hocalarım ve sevgili arkadaşlarım,
yazdığım sorular arasından biraz fazla hatalı soru çıktı bunun için kusura bakmayın. Bazı soruları yapamadığımda sorudan değil kendi yanlışımdan kaynaklandığını düşündüm bu yüzden sizlere sormak istedim bilemedim basım hatası olduğunu.
Karekök yayınlarında basım hatası fazla varmış, zaten değiştirdim yayını bunlar bu yayından son sorularım.
12 nolu soru:
İstenen bölge y=x-2 , x=4 ve x-ekseni arasında kalan bölgenin hacmi. Rondela-disk yöntemiyle,
V=pi. ∫ (x-2)2 dx from (2 to 4)
V=8/3 pi bulunur.
Vakit bulursak ötekilere de bakarız bir ara...
İstenen bölge y=x-2 , x=4 ve x-ekseni arasında kalan bölgenin hacmi. Rondela-disk yöntemiyle,
V=pi. ∫ (x-2)2 dx from (2 to 4)
V=8/3 pi bulunur.
Vakit bulursak ötekilere de bakarız bir ara...
16 soruda bir yerde hata yapıyorum ama bulamadım neresi hatalı
16 soruda bir yerde hata yapıyorum ama bulamadım neresi hatalı
Eee jenny çözdüğüm 12 nolu soruyu silmişsin, gözükmüyor, yoksa bende mi var bir problem, bilgisayarda...
16 nolu soruyu doğru çözmüşsünüz. y=0 demeseydi,
∏∫(ex)2dx (-∞ to ln2) = 2∏ eder.
16 nolu soruyu doğru çözmüşsünüz. y=0 demeseydi,
∏∫(ex)2dx (-∞ to ln2) = 2∏ eder.
5 no'lu son soru:
-y2=y2-8 ---> y1=2 , y2=-2
∫ (-y2-(y2-8))dy (-2 to 2) = 64/3 br2
Veya:
2.∫ (-y2-(y2-8))dy (0 to 2) = 64/3 br2
-y2=y2-8 ---> y1=2 , y2=-2
∫ (-y2-(y2-8))dy (-2 to 2) = 64/3 br2
Veya:
2.∫ (-y2-(y2-8))dy (0 to 2) = 64/3 br2
Eee jenny çözdüğüm 12 nolu soruyu silmişsin, gözükmüyor, yoksa bende mi var bir problem, bilgisayarda...
16 nolu soruyu doğru çözmüşsünüz. y=0 demeseydi,
∏∫(ex)2dx (-∞ to ln2) = 2∏ eder.
16 nolu soruyu doğru çözmüşsünüz. y=0 demeseydi,
∏∫(ex)2dx (-∞ to ln2) = 2∏ eder.
5 no'lu son soru:
-y2=y2-8 ---> y1=2 , y2=-2
∫ (-y2-(y2-8))dy (-2 to 2) = 64/3 br2
Veya:
2.∫ (-y2-(y2-8))dy (0 to 2) = 64/3 br2
-y2=y2-8 ---> y1=2 , y2=-2
∫ (-y2-(y2-8))dy (-2 to 2) = 64/3 br2
Veya:
2.∫ (-y2-(y2-8))dy (0 to 2) = 64/3 br2
Diğer çözümlü sorular alttadır.