Z²-2(1+i)Z+2i+4=0 eşitliğini sağlayan karmaşık sayılar Z₁ ve Z₂'dir.
Buna göre |1/Z₁-1/Z₂| ifadesi kaçtır=
2/√5 cevap
Buna göre |1/Z₁-1/Z₂| ifadesi kaçtır=
2/√5 cevap
2.soru
(Z-2-2i)üssü6=cisα eşitliğini sağlayan Z karmaşık sayılarından esas argümenti en küçük olan W karmaşık sayısıdır.
Buna göre |W| kaçtır?
√7 şimdiden teşekkürler
(Z-2-2i)üssü6=cisα eşitliğini sağlayan Z karmaşık sayılarından esas argümenti en küçük olan W karmaşık sayısıdır.
Buna göre |W| kaçtır?
√7 şimdiden teşekkürler
ComingSoon 21:30 25 Kas 2013 #3 Z²-2(1+i)Z+2i+4=0 eşitliğini sağlayan karmaşık sayılar Z₁ ve Z₂'dir.
Buna göre |1/Z₁-1/Z₂| ifadesi kaçtır=
2/√5 cevap
Buna göre |1/Z₁-1/Z₂| ifadesi kaçtır=
2/√5 cevap
x²-2(1+i)x+2i+4=0 diyoruz.Buradan Deltayı buluruz.Delta=b²-4ac idi.Yani
(-2(1+i))²-4(2i+4)=Delta
Deltayı -16 buluruz √delta=4i olur.
Daha sonra kökleri (-b±√delta)/2a'dan buluruz.
Buradan x₁ ve x₂=(2+2i±4i)/2 deriz buradan kökler 1-i ve 1+3i çıkar.Yani z₁ ve z₂ değerlerini bulduk.
Sonrasında |1/z1-1/z2|'yi bulursun.Onu yaparsın sen zaten.
buradan 1/z1-1/z2=(2+4i)/5 çıkar.Bunun modülü ise 2√5/5 yani 2/√5'tir.
Öncelikle Z yerine x dersek rahatlıkla ikinci dereceden denklemi görebiliriz.
x²-2(1+i)x+2i+4=0 diyoruz.Buradan Deltayı buluruz.Delta=b²-4ac idi.Yani
(-2(1+i))²-4(2i+4)=Delta
Deltayı -16 buluruz √delta=4i olur.
Daha sonra kökleri (-b±√delta)/2a'dan buluruz.
Buradan x₁ ve x₂=(2+2i±4i)/2 deriz buradan kökler 1-i ve 1+3i çıkar.Yani z₁ ve z₂ değerlerini bulduk.
Sonrasında |1/z1-1/z2|'yi bulursun.Onu yaparsın sen zaten.
buradan 1/z1-1/z2=(2+4i)/5 çıkar.Bunun modülü ise 2√5/5 yani 2/√5'tir.
x²-2(1+i)x+2i+4=0 diyoruz.Buradan Deltayı buluruz.Delta=b²-4ac idi.Yani
(-2(1+i))²-4(2i+4)=Delta
Deltayı -16 buluruz √delta=4i olur.
Daha sonra kökleri (-b±√delta)/2a'dan buluruz.
Buradan x₁ ve x₂=(2+2i±4i)/2 deriz buradan kökler 1-i ve 1+3i çıkar.Yani z₁ ve z₂ değerlerini bulduk.
Sonrasında |1/z1-1/z2|'yi bulursun.Onu yaparsın sen zaten.
buradan 1/z1-1/z2=(2+4i)/5 çıkar.Bunun modülü ise 2√5/5 yani 2/√5'tir.
Aşağıdaki karmaşık düzlemde Z₁ ve Z₁+Z₂ karmaşık sayıları çizilmiştir.
|Z₁|=|Z₁+Z₂| olduğuna göre,Arg(-i.Z₂) kaç derecedir?
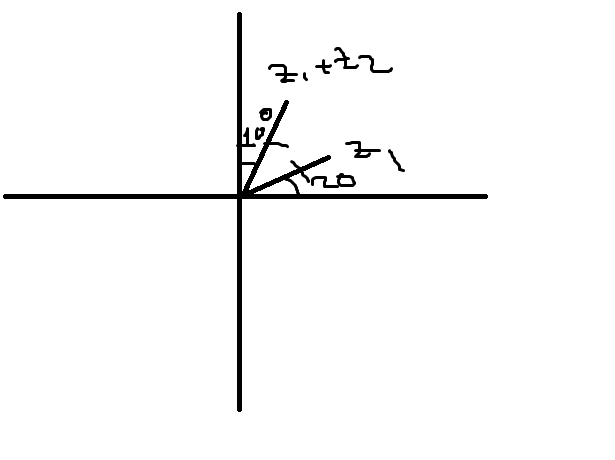
|Z₁|=|Z₁+Z₂| olduğuna göre,Arg(-i.Z₂) kaç derecedir?
ComingSoon 22:26 25 Kas 2013 #6 2.soru
(Z-2-2i)üssü6=cisα eşitliğini sağlayan Z karmaşık sayılarından esas argümenti en küçük olan W karmaşık sayısıdır.
Buna göre |W| kaçtır?
√7 şimdiden teşekkürler
(Z-2-2i)üssü6=cisα eşitliğini sağlayan Z karmaşık sayılarından esas argümenti en küçük olan W karmaşık sayısıdır.
Buna göre |W| kaçtır?
√7 şimdiden teşekkürler
z-2-2i=cis(a/6)
|z-2-2i|=|cis(a/6)|=1
|z-2-2i|=1 bir çember denklemidir.
Çemberin merkezinin orjine uzaklığı 2√2'dir.
W ise bu çemberin üzerindeki argümenti en küçük olan karmaşık sayıdır
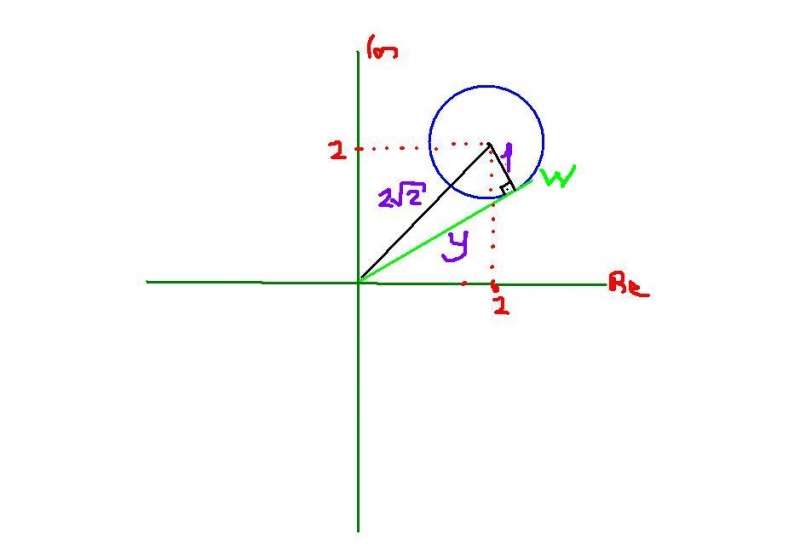
Pisagordan y²+1=8 çıkar ve y²=7 ve y=|w|=√7 olur.
ComingSoon 22:33 25 Kas 2013 #7 Aşağıdaki karmaşık düzlemde Z₁ ve Z₁+Z₂ karmaşık sayıları çizilmiştir.
|Z₁|=|Z₁+Z₂| olduğuna göre,Arg(-i.Z₂) kaç derecedir?
|Z₁|=|Z₁+Z₂| olduğuna göre,Arg(-i.Z₂) kaç derecedir?
ComingSoon 22:47 25 Kas 2013 #9
z₁=r.cis20
z₂=rcisα
z₁+z₂=r.cis80
Dönüşüm formüllerini uygularız.
rcis20+z₂=r.cis80 buradan sonra dönüşüm formülleri uygularız.
r(cos20+cosα+i(sin20+sinα))=rcis80
=r(2cos((20+a)/2).cos((20-a)/2)+i(2.sin((20+a)/2).cos((20-a)/2))=cis80
*2cos((20-a) parantezine alırız=> 2rcos((20-a)cis((20+a)/2)=rcis80
buradan (20+a)/2=80 olur.Yani 20+a=160 ve a=140.Buradan z₂=rcis140 olur.
Arg(-i.z₂)=Arg(-i)+Arg(z₂)=270+140=410.
410'un esas ölçüsü=50.Cevap 50
z₂=rcisα
z₁+z₂=r.cis80
Dönüşüm formüllerini uygularız.
rcis20+z₂=r.cis80 buradan sonra dönüşüm formülleri uygularız.
r(cos20+cosα+i(sin20+sinα))=rcis80
=r(2cos((20+a)/2).cos((20-a)/2)+i(2.sin((20+a)/2).cos((20-a)/2))=cis80
*2cos((20-a) parantezine alırız=> 2rcos((20-a)cis((20+a)/2)=rcis80
buradan (20+a)/2=80 olur.Yani 20+a=160 ve a=140.Buradan z₂=rcis140 olur.
Arg(-i.z₂)=Arg(-i)+Arg(z₂)=270+140=410.
410'un esas ölçüsü=50.Cevap 50
Sağol