|z-6i|=3
koşulunu sağlayan z karmaşık sayılardan argümenti en büyük olanın esas argümenti en az kaç radyandır?
koşulunu sağlayan z karmaşık sayılardan argümenti en büyük olanın esas argümenti en az kaç radyandır?
Cevap yok mu???
1) Verilen koşulu sağlayan karmaşık sayılar karmaşık düzlemde merkezi (0,6) ve yarıçapı 3 br olan bir çember belirtir.
Bu çembere teğet ve x ekseni ile pozitif yönlü en büyük açıyı yapacak olan doğruyu çizersek ve teğet oldukları için çemberin merkezinden doğruya bir dik çekersek, uzunlukları da hesaba kattığımızda 30-60-90 üçgenini görebiliriz.

Bu durumda|z-6i|=3 koşulunu sağlayan z karmaşık sayılardan argümenti en büyük olanın esas argümenti 120 derece=2∏/3 radyandır.
Bu çembere teğet ve x ekseni ile pozitif yönlü en büyük açıyı yapacak olan doğruyu çizersek ve teğet oldukları için çemberin merkezinden doğruya bir dik çekersek, uzunlukları da hesaba kattığımızda 30-60-90 üçgenini görebiliriz.

Bu durumda|z-6i|=3 koşulunu sağlayan z karmaşık sayılardan argümenti en büyük olanın esas argümenti 120 derece=2∏/3 radyandır.
Çok teşekkürler yarınki matematik sınavın hazırlanıyorum çok yardımcı oldu 
Rica ederim anlamadığınız bir yer varsa sorabilirsiniz.
anlamadığım bir yer yok bir de şu soruyu çözerseniz mutlu olurum:
Arg(z+5i)=pi/6 olmak üzere
|z-5i| ifadesinin en küçük değeri nedir?
Arg(z+5i)=pi/6 olmak üzere
|z-5i| ifadesinin en küçük değeri nedir?
Sorduğun sorunun cevabını da bizimle paylaşırsan önce kendi bilgimizin doğruluğunu teyid edip sonra sana yardımcı olmaya çalışırız 
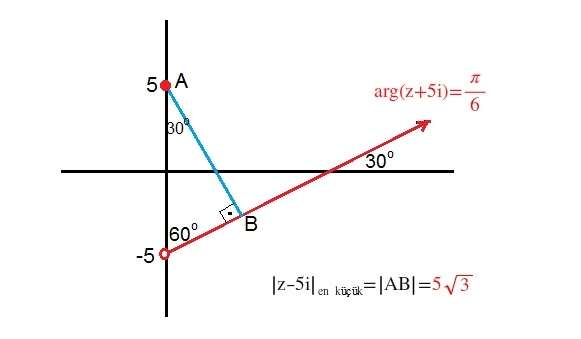
2) Arg(z+5i)=pi/6 olmak üzere |z-5i| ifadesinin en küçük değeri nedir?
Öncelikle z=x+yi diyelim. Bu durumda verilen açının tanjantı yani tan30 (y+5)/x e eşit olacaktır. (Sayıyı karmaşık düzleme aktararak işlem yaptık.)
Bu durumda y√3+5√3=x olacaktır.
|z-5i| ifadesininde z=x+yi ve y√3+5√3=x için yazarsak;
|x+(y-5)i|= |√3(y+5)+i(y-5)| olacaktır. Modülün değerini bulacak olursak;
√(√3(y+5))²+(y-5)²=
=√4y²+20y+100 olacaktır. Bu durumda modülün en küçük değerini parabolde tepe noktasının ordinatını bularak ;
(4ac-b²)/4a= (4.4.100-400)/16 = 75= 4y²+20y+100 parabolünün en küçük değeri olur.Değerin kökünü alırsak sonuç 5√3 olacaktır.
Öncelikle z=x+yi diyelim. Bu durumda verilen açının tanjantı yani tan30 (y+5)/x e eşit olacaktır. (Sayıyı karmaşık düzleme aktararak işlem yaptık.)
Bu durumda y√3+5√3=x olacaktır.
|z-5i| ifadesininde z=x+yi ve y√3+5√3=x için yazarsak;
|x+(y-5)i|= |√3(y+5)+i(y-5)| olacaktır. Modülün değerini bulacak olursak;
√(√3(y+5))²+(y-5)²=
=√4y²+20y+100 olacaktır. Bu durumda modülün en küçük değerini parabolde tepe noktasının ordinatını bularak ;
(4ac-b²)/4a= (4.4.100-400)/16 = 75= 4y²+20y+100 parabolünün en küçük değeri olur.Değerin kökünü alırsak sonuç 5√3 olacaktır.