http://k1311.hizliresim.com/1h/k/un74b.jpg
http://k1311.hizliresim.com/1h/k/un76b.jpg
http://m1311.hizliresim.com/1h/k/un76t.jpg
http://k1311.hizliresim.com/1h/k/un77j.jpg
http://u1311.hizliresim.com/1h/k/un7b0.jpg
5 soru var,resim seklinde ekleyince daha anlaşılır olacağını düşündüm
http://k1311.hizliresim.com/1h/k/un76b.jpg
http://m1311.hizliresim.com/1h/k/un76t.jpg
http://k1311.hizliresim.com/1h/k/un77j.jpg
http://u1311.hizliresim.com/1h/k/un7b0.jpg
5 soru var,resim seklinde ekleyince daha anlaşılır olacağını düşündüm
şimdilik cevaplıyorum ama bu şekilde fotoğraf ile soru sormak yasak.(yazılabilecek sorular için) moderatörleri kızdırmayalım 
1.soru
logf(x)g(x) şeklindeki bir logaritmanın en geniş tanım kümesi
f(x)>0 ,g(x)>0 ve f(x)≠1 durumları geçerli.
(x+2)²>0 olmalı. bu tüm reel sayılar için geçerlidir. bir sayının karesi her zaman pozitiftir.
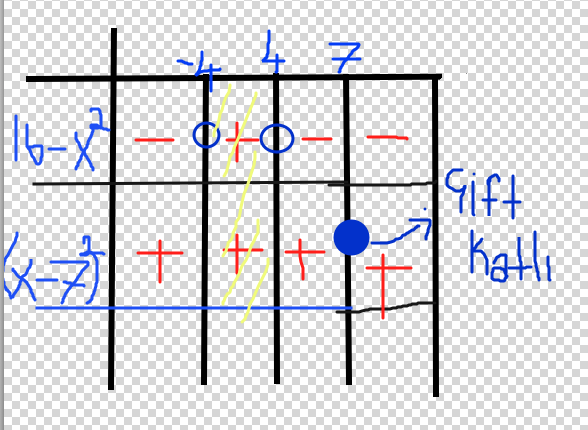
(16-x²)/(x-7)²>0 olmalı. burada eşitsizlikten kök bulun ve tablo yapın.,
x=±4 ve x=7 gelir.

bu tablodan en geniş tanım kümesi (-4,4) aralığı fakat bir de
(x+2)²≠1 durumu var. burayı yanlış hatırladım
her iki tarafın karekökünü alın.
|x+2|≠1 mutlak değerden kurtarın.
x+2≠1 ve x+2≠-1 gelir.
x≠-1 ve x≠-3 durumu gelir. bunu tanım aralığından çıkaracaksın.
(-4,4)-{-3,1}
1.soru
logf(x)g(x) şeklindeki bir logaritmanın en geniş tanım kümesi
f(x)>0 ,g(x)>0 ve f(x)≠1 durumları geçerli.
(x+2)²>0 olmalı. bu tüm reel sayılar için geçerlidir. bir sayının karesi her zaman pozitiftir.
(16-x²)/(x-7)²>0 olmalı. burada eşitsizlikten kök bulun ve tablo yapın.,
x=±4 ve x=7 gelir.
bu tablodan en geniş tanım kümesi (-4,4) aralığı fakat bir de
(x+2)²≠1 durumu var. burayı yanlış hatırladım
her iki tarafın karekökünü alın.
|x+2|≠1 mutlak değerden kurtarın.
x+2≠1 ve x+2≠-1 gelir.
x≠-1 ve x≠-3 durumu gelir. bunu tanım aralığından çıkaracaksın.
(-4,4)-{-3,1}
2.soru
verilen fonksiyonun tanım aralığını log ifade belirler. yukarıda yaptığım gibi yapacağız gene.
x²+x+1>0 olmalı. köklerini bulmak için ∆ bakın.
∆<0 geldi.(∆=b²-4ac (ax²+bx+c=0 gibi bir denklemde))
∆<0 ve başkatsayı pozitif olduğu için bu ifade tüm reel sayılar için pozitiftir. yani tanım aralığı tüm reel sayılar. R
verilen fonksiyonun tanım aralığını log ifade belirler. yukarıda yaptığım gibi yapacağız gene.
x²+x+1>0 olmalı. köklerini bulmak için ∆ bakın.
∆<0 geldi.(∆=b²-4ac (ax²+bx+c=0 gibi bir denklemde))
∆<0 ve başkatsayı pozitif olduğu için bu ifade tüm reel sayılar için pozitiftir. yani tanım aralığı tüm reel sayılar. R
3.soru
ilk soru ile aynı yolla yapılacak.
(x²-4)/x²>0 1. eşitsizlik/ (x²-4)/x²≠1 olmalı.
√1-|x+2|>0 olmalı. 2. eşitsizlik
kareköklü ifadeler her zaman pozitif çıkmalı. bunun için kökün içi pozitif olmalı. yani
1-|x+2|>0 olmalı.
-|x+2|>-1
|x+2|<1 gelir. mutlak değerden kurtarırsanız
-1<x+2<1 gelir.
-3<x<-1 gelir. yani 2. eşitsizliğin çözüm aralığı (-3,-1)
1. eşitsizlik için
x²-4=0
x=±2 gelir paydaya bakma. x² olsuğu için sürekli pozitif değer çıkar. fakat x=0 için belirsizlik olur. yani x=0 olmamalı.

buradan da (-∞,-2)u(2,∞) gelir.
en geniş tanım aralığı iki aralığın birleşimidir.
(-3,-2) aralığı.
ilk soru ile aynı yolla yapılacak.
(x²-4)/x²>0 1. eşitsizlik/ (x²-4)/x²≠1 olmalı.
√1-|x+2|>0 olmalı. 2. eşitsizlik
kareköklü ifadeler her zaman pozitif çıkmalı. bunun için kökün içi pozitif olmalı. yani
1-|x+2|>0 olmalı.
-|x+2|>-1
|x+2|<1 gelir. mutlak değerden kurtarırsanız
-1<x+2<1 gelir.
-3<x<-1 gelir. yani 2. eşitsizliğin çözüm aralığı (-3,-1)
1. eşitsizlik için
x²-4=0
x=±2 gelir paydaya bakma. x² olsuğu için sürekli pozitif değer çıkar. fakat x=0 için belirsizlik olur. yani x=0 olmamalı.
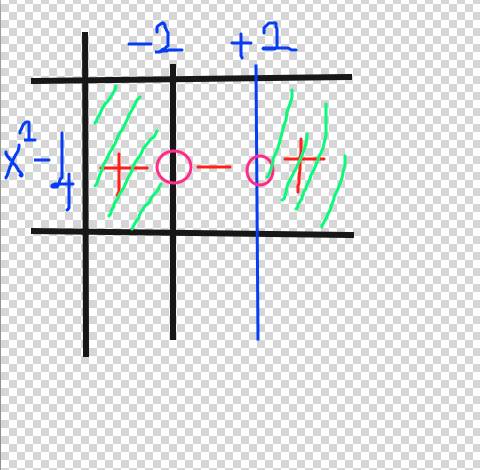
buradan da (-∞,-2)u(2,∞) gelir.
en geniş tanım aralığı iki aralığın birleşimidir.
(-3,-2) aralığı.
4.soru
önce a değerini bulmalısınız. bunun için grafikten yardım alın. dikkat! grafik x değerlerini kapsar. x-2 değerlerini değil.
x=4 için y=2 değerine gitmiş. yerine yaz.
loga(4-2)=2
a2=2
a=√2 gelir. (ax=b ise logab=x olur. buradan geldi)
f(x)=log√2(x-2)
x=10 için yani f(10)=log√2(10-2)=log√28
8=√26 olur. yerine yazarsan cevap 6 gelir.
önce a değerini bulmalısınız. bunun için grafikten yardım alın. dikkat! grafik x değerlerini kapsar. x-2 değerlerini değil.
x=4 için y=2 değerine gitmiş. yerine yaz.
loga(4-2)=2
a2=2
a=√2 gelir. (ax=b ise logab=x olur. buradan geldi)
f(x)=log√2(x-2)
x=10 için yani f(10)=log√2(10-2)=log√28
8=√26 olur. yerine yazarsan cevap 6 gelir.
Bilmiyordum,çok sağolun
Bide bizim resim yükleme aracımız var onunla yükleyiniz (şekilli sorularınızı).
