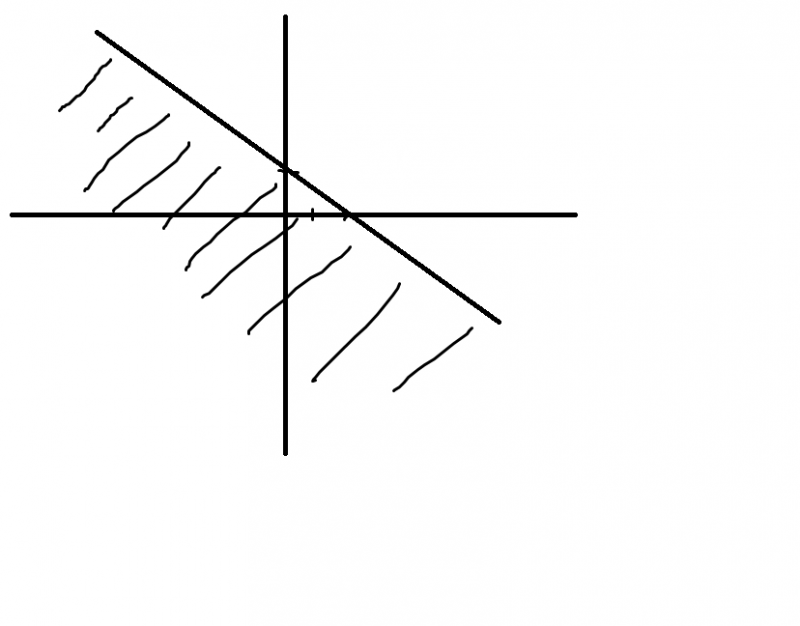
1) z|z∈C, |z|+im(z)≤2 karmaşık sayısını karmaşık düzlemde gösteriniz.
2) z|z∈C, |z+3i|≤|z+6-5i|kümesini karmaşık düzlemde gösteriniz.
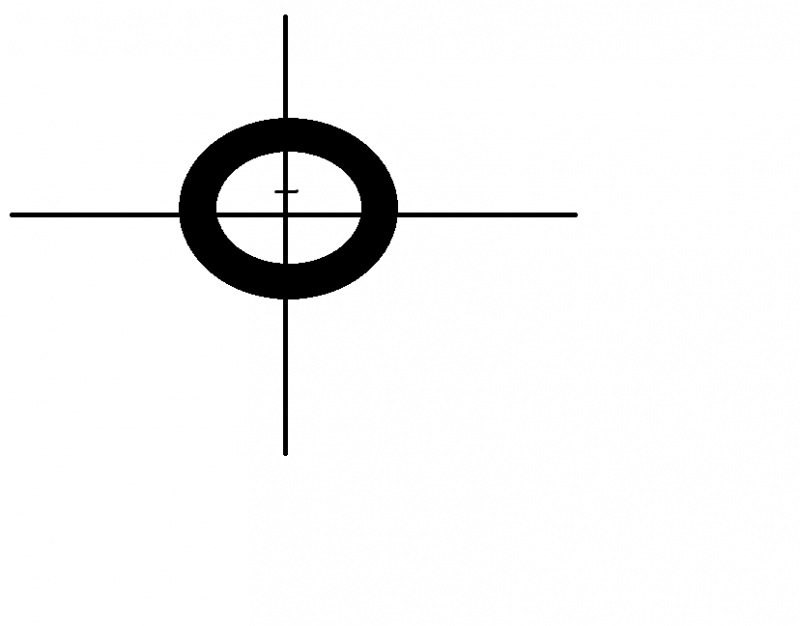
3) 3≤|z-i|<5 karmaşık düzlemde oluşturduğu bölgenin alanını bulunuz.
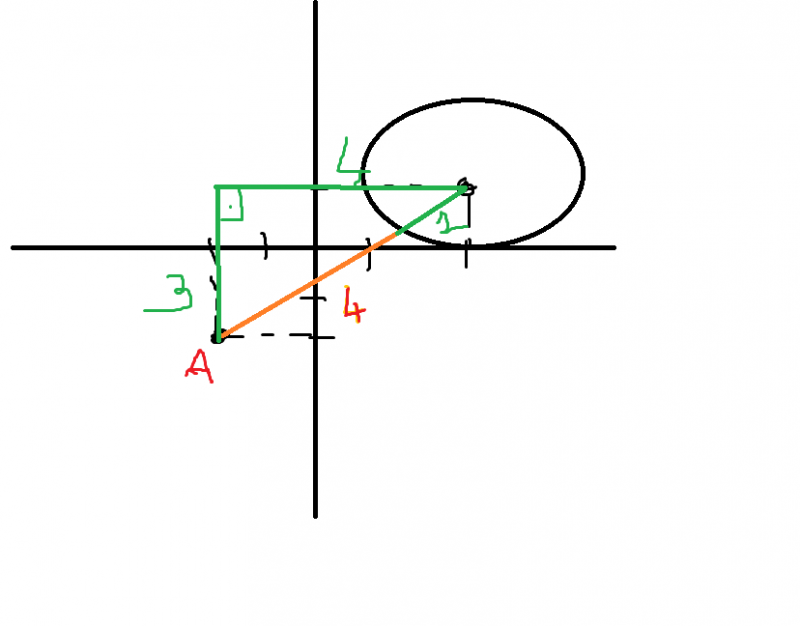
4) |z-2-i|≤1 olduğuna göre |z+2+2i| ifadesinin alabileceği en küçük değeri bulunuz.
5) z[2(cos9+isin9)]üssü10 / [2(cos10+isin10)]üssü12 ise z=a+bi yi bulunuz.