Olasılık soruları

1) Bir çubuk rastgele kırılıp iki parçaya ayrılıyor. Bu parçalardan uzun olan parçanın, kısa olan parçanın en az 2 katı uzunlukta olma olasılığı kaçtır?(2/3)


2)Daire biçimindeki bir poligona atış yapan atıcı tüm atışlarını daireye isabet ettirmiştir. Buna göre atıcının yaptığı bir atışta dairenin çevresine değil merkezine daha yakın olma olasılığı kaçtır?(1/4)


3)4 mektup, 5 ayrı posta kutusuna rastgele atılıyor. Mektupların her birinin farklı kutulara atılmış olma olasılığı kaçtır?(1/5)


4)Bir kenar uzunluğu 2 cm olan bir düzgün altıgenin içinden seçilen bir noktanın köşelere olan uzaklığının 1cm ve 1cmden küçük olma olasılığı kaçtır?(√3.∏/9)


5)Altı yüzüde mavi boyalı olan küpün bir ayrıtı 4 cmdir. Bu küp ayrıtları 1cm olan küplere bölünüyor ve bu köplerden biri rastgele seçiliyor. Seçilen küpün üzerinde boya olmama olasılığı kaçtır?(1/8)


Şimdiden teşekkürler.

1) Çubuğun uzunluğu L olsun. Parçalardan birinin uzunluğu x olursa diğeri L-xx olsun. 0≤x≤L olduğuna dikkat edelim. Uzun parça x olursa x ≥ 2(L-x) ve buradan da x≥2L/3 olmalı. Uzun parça L-x olursa L-x≥2x ve buradan da x ≤ L/3 olmalı. Yani x∈[0, L/3]∪[2L/3, L] olursa uzun parça kısa parçanın en az iki katı olur. İstenen olasılık 2/3 tür.

2) Dairenin yarıçapı 2r olsun. Merkezi bu dairenin merkezi ve yarıçapı r olan bir daire düşünün. (Yani bu dairenin içine aynı merkezli yarıçapı büyük dairenin yarıçapının yarısı olan bir daire düşünün.) İstenen olasılık içerideki küçük dairenin isabet ettirilmesi olasılığıdır. İçerideki dairenin alanı büyük dairenin alanının dörtte biri olduğuna göre istenen olasılık 1/4 tür.

3) İstenen durumun olması için posta kutularından birinin boş kalması yeterli olacaktır. Yani sadece bir posta kutusunun boş olma olasılığına bakmamız gerekiyor. 5 posta kutusundan sadece 1'inin boş olma ihtimali 1/5 tir.

4) Bu soru çözülmüştü: Altıgenin köşelerine yarıçapları 1 br olan altıda birlik daire dilimleri çizelim. Daire dilimlerinin toplam alanı = 2 tane dairenin alanı = 2 pi

altıgenin alanı = 6√3

istenen olasılık 2 pi / 6√3 = √3 pi / 9

5) 4.4.4 tane birim küp vardır. Bunlardan boyalı olmayanlar merkezdekilerdir ve bunların sayısı 2.2.2 dir. İstenen olasılık 2.2.2/(4.4.4) = 1/8 olur.

"Uzun parça x olursa x ≥ 2(L-x) ve buradan da x≥2L/3 olmalı. Uzun parça L-x olursa L-x≥2x ve buradan da x ≤ L/3 olmalı."

burasını biraz daha açar mısınız?

uzun parçanın uzunluğu kısa parçanın uzunluğunun en az iki katı olmalı denmiş soruda. Uzun oarça x, kısa parça L-x olursa x ≥ 2(L-x) olmalı. Diğeri de aynı.

Soruyu farklı olarak şöyle de düşünebilirsiniz. Çubuğun uzunluğu 2L olsun. x∈[0, L] olmak üzere uzun olan parça yarıdan x kadar fazla olsun. Yani uzun parça L+x olsun. Bu durumda kısa parça L-x olur. Uzun≥ 2kısa olması gerektiğinden L+x ≥ 2(L-x) buradan da x≥ L/3 olur. Yani aradığımız şart için x∈[L/3, L] olmalı. [L/3, L] aralığının uzunluğu [0, L] aralığının uzunluğuna oranı = 2/3.

teşekkür ederim.

cevaplar için çok teşekkürler

"Yani x∈[0, L/3]∪[2L/3, L] olursa uzun parça kısa parçanın en az iki katı olur. İstenen olasılık 2/3 tür." hocam burdan nasıl 2/3 çıktığını anlayamadım biraz açar mısınız?

2. cevabınızdada poligonun 2 daireli olduğunu nasıl biliyoruz

Bilmiyoruz oraya hayali ikinci bir daire biz çizdik. Ve içerideki daireyi isabet ettirirsek, merkeze daha yakın vurmuş oluruz.

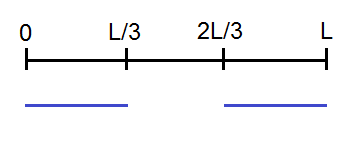
şekilde mavi çizgilerin uzunlukları toplamı / siyah çizginin uzunluğu=2/3