Permütasyon

1-)
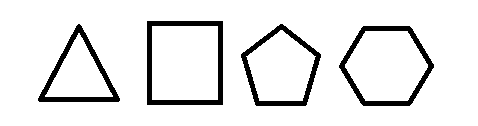
Fatma her şekil diğerinden farklı renkte olacak biçimde yukarıdaki şekilleri boyayacaktır. Fatma'nın farklı renklerde 6 boya kalemi olduğuna göre, bu boyama işlemi kaç farklı şekilde yapılabilir? Cevap C

A)180 B)240 C)360 D)420 E)480

2-){1,2,3,4,5,6} kümesinin elemanları ile rakamları farklı beş basamaklı sayılar yazılacaktır. Bu sayılardan aç tanesinde 1 ile 5 ve 2 ile 6 yan yanadır? Cevap D

A)32 B)36 C)40 D)48 E)52

3-){0,1,2,3,4} kümesinin elemanları ile üç basamaklı, rakamları farklı ve 4 ile tam bölünebilen kaç farklı sayı yazılabilir? Cevap C

A)13 B)14 C)15 D)16 E)17

4-)A={0,1,2,3,4,5} kümesinin elemanları ile 3 basamaklı, 3 ile bölünebilen ve rakamları farklı olan kaç sayı yazılabilir? Cevap A

A)40 B)36 C)24 D)20 E)18

5-)A={1,2,3,4,5,7} kümesinin elemanları kullanılarak tek ve çift rakamların kendi aralarında küçükten büyüğe doğru sıralandığı rakamları farklı ve altı basamaklı kaç farklı doğal sayı yazılabilir? Cevap C

A)10 B)12 C)15 D)18 E)20

Şimdiden teşekkürler..

C-5
Tekleri kendi aralarında 1,3,5,7 yüzlerine siyah çorap geçirelim.Aynı şekilde çiftlere de 2,4'e geçirelim xxxxyy => 6!/4!.2! = 6.5/2 = 15 şekilde dizilirler.

C-4

1+2+0=0 mod 3 şartını sağlamalı sayılarımız aksi taktirde olmuyor.
3 ile bölündüğünde 1 kalanı verenler => 1,4'tür.Bunlardan birini seçelim.C(2,1)=2
3 ile bölündüğünde 2 kalanı verenler 2,5'tir.C(2,1)=2
Aynı şekilde 0 kalanı verenler 0,3'tür.C(2,1)=2 tane sayı seçilebilir.
Kendi aralarınad 2.2.2 => 8 tane sayı seçilebilir Bunları 3! kadar dizeriz. 6.8=48 diziliş olur 0 ile başlayanları çıkaralım 0 _ _ => 4 tane seçeriz 2 şekilde dizeriz 48-8=40 tane bulunur.

C-2

1-5'i iple yanyana bağlıyalım.2 ile 6'yı iple yanyana bağlıyalım. (15)(26)x => x'i 2 şekilde seçebiliriz. 3! kadar dizilirler. C(2,1).3!.2!.2! => 1-5 kendi arasında 2 şekilde dizilir , 2 - 6 kendi arasında 2 şekilde dizilir.

C-3
4 ile tam bölünebilmesi için son basamak 04 olabilir.
12,24,32 ,40 olabilir.
_ 04 => Başa 3 tane seçebilir.=> 3 tane sayı yazılabilir.
_ 12 => başa 3,4 gelebilir => 2 tane.
_ 24 => Başa 2 tane gelebilir.
_32 => Başa 2 tane gelebilir.
_40 => Başa 3 tane gelebilir.
_20 => başa 3 tane gelebilir.
15 tane yani.

1)6 renkten 4ünü C(6,4)=15 farklı şekilde seçeriz. Seçtikten sonra 1.boyayı 4şekilden biri 2. boyayı 3şekilden biri 3.boyayı 2 şekilden biri 4.boyayı kalan son şekil için kullanırız. 15.4.3.2=360

Alternatif olarak.
1.
Burada ilk şekil 6 şekilde , ikinci 5 şekilde , üçüncü 4 şekilde , ikinci 3 şekilde boyanabilir.(Farklı olmaları istendiğinden böyle diyoruz.)
6.5.4.3 = 360

5.
Tekler 1,3,5,7'dir tüm dizilişlerin 1/4! kadarında bunlar istenilen sıradadır.
Yine bunların 1/2! kadarında 2,4 ile istenilen sıradadır 6!/4!.2! = 15 şekilde yani.

Çok teşekkürler arkadaşlar çok hızlısınız

Rica