Karmaşık Sayılar

1)arg[z.(1+i)]=3∏/4 olduğuna göre arg(z²) kaç radyandır? (Doğru cevap B şıkkı.)

A)∏/2 B)∏ C)3∏/2 D)4∏/3 E)2∏

2)

(Doğru cevap D şıkkı.)

3)z=i+cos40+isin40 karmaşık sayısının esas argümenti ? (Doğru cevap E şıkkı.)

A)20 B)25 C)40 D)50 E)65

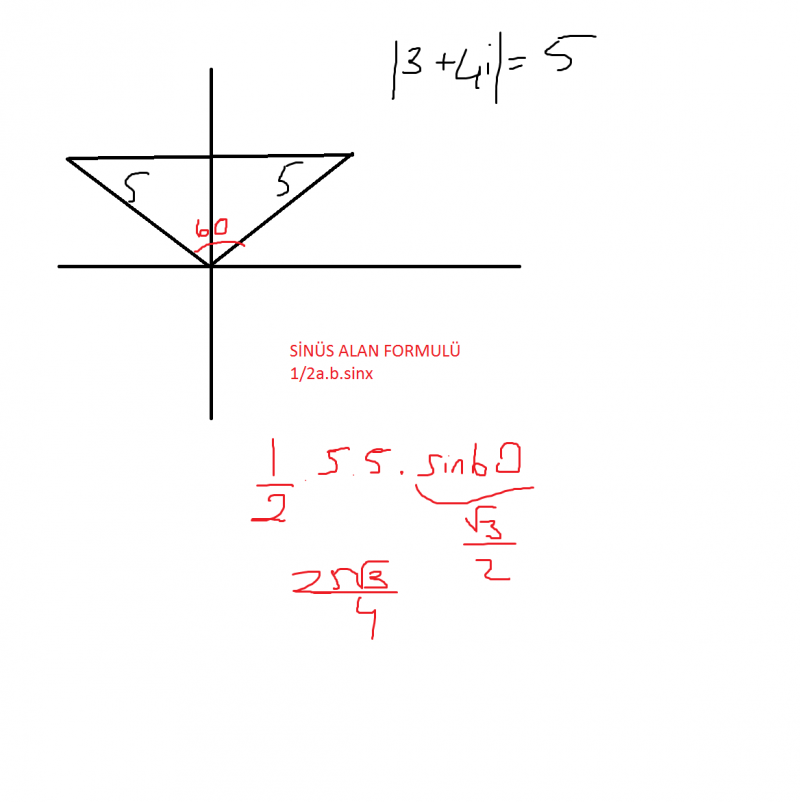
4)z₁=3+4i karmaşık sayısının orijin etrafında pozitif yönde 60 derece döndürülmesi ile elde edilen karmaşık sayı z₂ olduğuna göre z₁Oz₂ üçgeninin alanı kaç birimkaredir? (Doğru cevap C şıkkı.)

A)25/2 B)25/4 C)(25√3)/4 D)5/2 E)25/(2√3)

5) z⁴=16i eşitliğini sağlayan z karmaşık sayıları z₁,z₂,z₃,z₄ olduğuna göre arg(z₁.z₂) aşağıdakilerden hangisi olamaz?
(Doğru cevap D şıkkı.)

A)45 B)135 C)225 D)295 E)315

Şimdiden teşekkürler..

argümentlerde çarpımda dereceler toplanır yani
Arg(z1)+Arg(1+i)=135 1+i cis 45'tir
Arg(z1)=135-45
90 derece bulunur karesini alırken de üs ile derece çarpılırsa yani 90.2 o da 180 olarak bulunur

i+cos40+isin40 i'yi cis90 olarak yani cos90+isin90 olarak yazalım
cos90+isin90+cos40+isin40
cos90+cos40+i(sin90+sin40) burda geçen seneki dönüşüm formüllerini kullanıcaz
2cos65.cos25+i(2sin65.cos25) 2cos25 parantezine alalım
2cos25(cos65+isin65) argümenti 65 boyu da 2cos25 olarak bulundu

5. soruda bir tuhaflık mı var 45 de olmuyor 295 de

Bence de bir şey var galiba 135 225 315 oluyor ama diğerleri olmuyor belki bilmediğimiz bir şey vardır ?

16cis90'nın 4. dereceden kökleri 2cis22.5 2cis112.5 2cis202.5 2cis292.5 burdan 45 nasıl çıkar ki 22,5+22,5 45 olur ama niye öle olsun ki