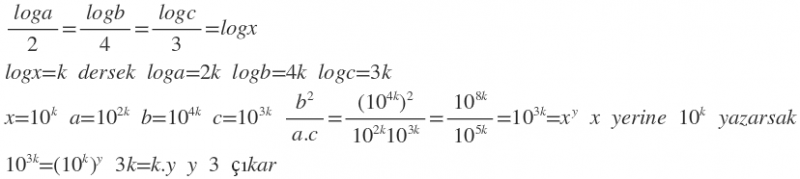Logaritma

1) e^lna.logax = x²-3x+4 ise x =? (2)

2) log₂(8-x²) = 10^log(3-x) denkleminin çöz. küm. elm. birisi=? (0)

3) loga/2 = logb/4 = logc/3 = logx ve b²/ac = x^y ise y=? (3)

4) a=log₃x, b=log₄x, c=log₅x ise a.b.c= a.c + a.c+ b.c yi sağlayan x değeri=? (60)

5) Reel sayılar kümesinde x^√x = (√x)^x denk. çözüm kümesi=? ( 1,4 )

C-1)

Sanırım, 2. çarpanın tabanı a olacaktı.

Bu ifadeyi (e^lna)^log_ax yazalım logaritmadaki üslü sayı özelliğinden,

(a^lne)^log_ax olur.

=a^log_xa yine aynı özellikten bu ifade x olur.

x=x²-3x+4

x²-4x+4=(x-2)²=0 ise x=2 bulunur.

C-2)

log₂(8-x²)=10^log(3-x) olduğundan, bir önceki soruda yaptığımız gibi eşitliğin sağ tarafına bu özelliği uygulayalım.

log₂(8-x²)=(3-x)¹ olacaktır.

2^3-x=8-x²

Burada değer vererek görebiliriz.

Ya da (8-x²)>0 x≠1 denkleminden de görülebilir.

maalesef yapamadım hiçbirini okulda yeni geçtik...

evet basım hatası varmış kitapta.

Tamamdır.
Fizik yazılısına çalışmam gerek, çözen olmazsa geldiğimde bakarım diğerlerine

C-3)


loga/2 = logb/4 = logc/3 = logx ve b²/ac = xy ise y=? (3)

Oran orantının özelliğinden,

loga/2=logc/3=logb/4 ise

loga+logc/5=logb/4

log(a.c)=(5/4)*logb ise

a.c=b^(5/4) olur.

Şimdi de, b'yi x cinsinden bulalım.

logb/4=logx ise b=x⁴ olur.

b²/ac=b²/b^(5/4)=x^y ise

b^3/4=x^y

(x⁴)^(3/4)=x^y

ise y=3 bulunur.

2 farklı çözüm oldu. Soru güzel. Sanırım finalden/formul/fdd den bu soru

duygu 95 o oran orantı özelliği ne

9. Sinifta ogrendiniz mi bilmiyorum.

a/b=c/d=k olsun

(a+c)/(b+d)=k olur.

Ayrica 3 lu durumlarda ikiser veya ucer de esitlenebilir