çözümleri de yazsanız müthiş olcak da
çözümleri de yazsanız müthiş olcak da
ben de çözdüm
C-5
|z⁻¹|=|1/z| olarak yazalım, ayrı ayrı modül alabildiğimizden, |1|/|z| olarak da yazılabilir, bunun da eşiti 1/|z| olacaktır.
|z|+z.1|z|=2+i
Payda eşitlersek,
|z|²+z|z|=2+i
|z|²+z=|z|.(2+i)
z=x+yi olsun.
|z|=√x²+y²
|z|²=x²+y²
x²+y²+x+yi=√x²+y².(2+i)
x²+y²+x+yi=2√x²+y²+i√x²+y²
Her iki tarafın imajiner kısmı eşit olması gerektiğinden,
yi=i√x²+y²
y=√x²+y²
Kare alırsak,
y²=x²+y²
x²=0
x=0 bulunur.
Her iki tarafın reel kısmı da eşit olacak,
x²+y²+x=2√x²+y²
x=0 olduğundan,
y²=2√y²
y²=2y
y≠0 olduğundan sadeleştirme yapılabilir.
y²=2y
y=2 bulunur.
Sayımız z=x+yi
z=2i olacaktır.
Mathematics is the language of nature.
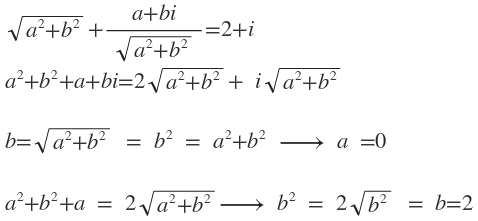
ben byi -2 de buldum
Bende 2i buldum.
Z=a+bi olsun.
|z|+z.|1/z|=2+i
√a²+b²+ a²+b².1/√a²+b²=2+i
2+i=a²+b²+a+a+bi/√a²+b²
1=b/√a²+b²
a²+b²=b²
a=0
a²+b²+a=2√a²+b²
b²=2√b²
b=2
Z=2i
Hata yapmışsın orada kare almayacaksın işte. Kare aldığın zaman olmayan kökler türetiyorsun.khorkhurt'den alıntı
ben byi -2 de buldum
Şöyle örnek veriyim,
x=3 olsun,
x²=9 olacaktır,
x²-9=0
x=±3 diyebilir misin?
Zaten işleme başlarken x=3 diye tanımlamıştık -3 diye bir kök yoktu değil mi
evet -2yi yerine koyunca olmuyor ama karesini almak mantıklı değil mi
Şöyle örnek veriyim,
x=3 olsun,
x²=9 olacaktır,
x²-9=0
x=±3 diyebilir misin?
Zaten işleme başlarken x=3 diye tanımlamıştık -3 diye bir kök yoktu değil mi
Foruma üye olmana gerek yok! Facebook hesabınla yorumlarını bekliyoruz!
